Другие виды зацепления 3 страница

= L_BC ω₂ / ω₁ .

Значения ω₂ берутся из имеющегося в нашем распоряжении графика ω₂(φ₂).

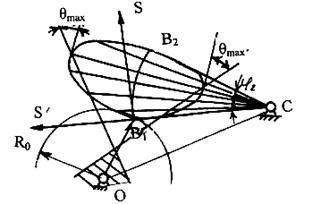
Рис. 6.11. - Определение минимального радиуса в кулачковом механизме с коромыслом

На фазе подъема аналоги скоростей откладываются от центра С, на фазе опускания - к центру. В точках, где аналоги скоростей максимальны, строятся перпендикуляры к лучам и к ним под допустимым углом давления проводятся прямые линии.

Если выбрать центр вращения кулачка в заштрихованной зоне, то отрезок ОВ₁ можно принять за минимальный радиус. В таком случае приближенно будет удовлетворяться допустимый угол давления. Выбрав положение очки О, мы тем самым определяем еще один размер механизма – расстояние между центрами вращения кулачка и коромысла – точками О и С.

6.9. Определене размерлов кулачквого механизма с тарельчатым толкателем

Если из-за размерных ограничений не удается поставить ролик или он оказывается недолговечным, применяют тарельчатый (плоский или несколько выпуклый) толкатель. Из условия контакта толкателя со всеми точками профиля следует, что кулачок должен быть везде выпуклым. Далее будет показано, что условие выпуклости связано с минимальным радиусом R₀. Заметим, что для данного вида кулачкового механизма угол давления во всех положениях равен нулю и, следовательно, не может служить для выбора R₀.

Известным способом построим мгновенный заменяющий рычажный механизм OABC (синусный механизм) и запишем уравнение, связывающее ускорения точек B₂ и B₁.

(6.2).

Построим соответствующий план ускорений в масштабе кривошипа и перенесем его на схему механизма, как показано на рис.6.12.

Рис.6.12. План ускорений кулачкового механизма

Величина масштабного коэффициента плана ускорений определится по формуле

k_a = ω²_k k_l,

где k_l – масштабный коэффициент кинематической схемы механизма.

Используя введенные масштабные коэффициенты, можно записать:

.

Параметр s˝ принято называть аналогом ускорений. Его связь с другими параметрами устанавливается следующим образом:

a = s˝ω²_k + s΄ ε. (6.3)

При равномерном вращении кулачка ε =0, тогда s˝ =a / ω²_k. Таким образом, на основании формулы (6.3) и рис.6.12 установлено, что истинное значение отрезка pb₂ представляет аналог ускорения s˝.

Условие выпуклости кулачка математически выражается неравенством ρ≥ 0, где ρ – радиус кривизны профиля кулачка. Из построения на рис 6.3 следует:

s˝ + R₀ + s = ρ ≥ 0,

откуда

R₀ ≥ - s″- s. (6.4)

Формула (6.4) устанавливает связь между условием выпуклости кулачка и минимальным радиусом.

Графический метод определения R₀ на основе формулы (6.4) состоит в следующем. Строится график S″ (S) и через точку с максимальной абсциссой на отрицательной ветви графика под углом 45˚ к оси проводится прямая линия до пересечения с осью ординат (рис. 6.13).

Рис. 6.13 Определение минимального радиуса

Если принять отрезок О₁О за R_O в масштабе k_s = k_{s ˝}, то из рассмотрения образующегося здесь равнобедренного прямоугольного треугольника вытекает соотношение: R₀ = - (s˝ - s΄).

Чтобы выполнялось условие (6.4), принимают R₀ несколько большей величины.

6.9. Построение профиля кулачка по заданному закону движения толкателя

Профиль кулачка представляет совокупность отдельных точек. Для его построения нужно знать координаты этих точек. Удобнее всего пользоваться полярной системой координат, т.е. задавать положение

каждой точки направлением радиус-вектора и величиной (модулем). Исходя из заданного закона ускорения получают закон перемещения толкателя и на его основе определяются координаты точек профиля.

Рассмотрим графический метод синтеза профиля для центрального кулачкового механизма с роликовым толкателем (рис. 6.14). Пусть задан график s(φ), минимальный радиус центрового профиля R₀, радиус ролика r. В выбранном масштабе k _l строится окружность минимального радиуса. Ось абсцисс графика и окружность минимального радиуса делится на равные части. Через точки деления из центра окружности проводятся лучи, выражающие положение оси толкателя в обращенном движении. Вдоль этих лучей от окружности минимального радиуса откладываются перемещения толкателя, взятые как соответствующие ординаты графика s (φ). Соединив полученные точки плавной кривой, получим центровой профиль. Действительный профиль строится внутри центрового профиля на расстоянии, равном радиусу ролика. Как видно из этого описания, синтез производится в порядке, обратном графическому анализу.

Рис. 6.14. Построение профиля центрального кулачкового механизма с роликовым толкателем

Для изготовления кулачка нужен не чертеж профиля, а координаты точек центрового профиля, совпадающих с центром фрезы. Нетрудно установить, что полярные координаты точек профиля определяются выражениями: R = R₀ + s (φ); β = φ,

где R - модуль радиус-вектора; β - полярный угол; φ - угол поворота кулачка.

Синтез профиля кулачка дезаксиального механизма производится подобным же образом. Отличие состоит лишь в том, что перемещения толкателя откладываются от окружности минимального радиуса вдоль

линий, касательных к окружности дезаксиала. Эти линии представляют положения оси толкателя в обращенном движении (рис. 6.15).

Рис.6.15. Построение профиля кулачка дезаксиального кулачкового механизма

При синтезе профиля кулачка для механизма с коромыслом задаются: закон движения в виде графика φ₂ (φ_k), длина коромысла L_BC, расстояние между центрами вращения кулачка и коромысла L_OC, радиус ролика r. В выбранном масштабе строится окружность минимального радиуса и концентрично ей окружность радиуса L_{OC ,} представляющая траекторию т. С в обращенном движении. Эта окружность разбивается на равные части, так же как и ось φ_k графика. Строится траектория т. В в виде дуги окружности радиуса L_BC и разбивается на участки, пропорциональные углам поворота коромысла φ₂. Через точки деления проводятся концентрические окружности. Из точек равномерного деления окружности радиуса L_OC делаются засечки радиусом коромысла L_BC на соответствующих концентрических окружностях. Полученные точки определяют центровой профиль кулачка.

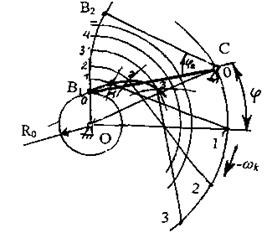
Рис. 6.16. Построение профиля кулачка для коромыслового кулачкового механизма

Для кулачкового механизма с тарельчатым толкателем перемещения тарелки, взятые с графика, откладываются на радиальных прямых, проведенных из центра окружности минимального радиуса (рис.6.17). Эти прямые представляют положения оси толкателя в обращенном движении. Через найденные точки проводятся линии, перпендикулярные оси толкателя и представляющие положения тарелки толкателя. Профиль кулачка строится как огибающая множество положений тарелки. Отметим, что точка касания профиля и тарелки не совпадает с точкой пересечения профиля и оси толкателя.

Рис. 6.17. Построение профиля кулачка для механизма с тарельчатым толкателем

Формулы для расчета координат центрового профиля для рассмотренных выше вариантов кулачковых механизмов приводятся в справочных пособиях (см., например, О.Н. Левитская, Н.И.Левитский. Курс теории механизмов и машин. - М., “Высшая школа”, 1978).

Действительный профиль кулачка строится внутри центрового профиля на расстоянии, равном радиусу ролика. Радиус ролика выбирается из конструктивных, а также технологических соображений, однако при этом следует учитывать возможность заострения действительного профиля кулачка.

Для выпуклого участка центрового профиля соответствующий участок действительного профиля также должен быть выпуклым. В противном случае возникает заострение действительного профиля.

Условие заострения на основании известной связи между двумя эквидистантными профилями можно выразить неравенством

ρ = ρ₀ – r ≥ 0,

где ρ₀ – радиус кривизны центрового профиля; ρ – радиус кривизны действительного профиля; r – радиус ролика.

Обычно принимается r = 0.7 ρ_0min. При больших радиусах кривизны, когда заострение неопасно, радиус ролика выбирается в зависимости от минимального радиуса центрового профиля по формуле r = 0.4 R₀.

6.10. Динамический анализ кулачковых механизмов

В теории механизмов и машин звенья механизмов обычно считаются абсолютно жесткими. Это несомненно представляет идеализацию физической картины, так как сама природа сил взаимодействия состоит в деформациях этих звеньев. В тихоходных механизмах эффект упругости звеньев практически не заметен. Однако в быстроходных механизмах, например в кулачковых механизмах привода клапанов автомобильных двигателей, учет упругости весьма существенно изменяет кинематические и динамические характеристики. Влияние упругости звеньев можно обнаружить только при рассмотрении динамики механизма.

Динамическое исследование начинается с выбора динамической модели. Эта модель всегда выбирается с некоторым упрощением, отражающим только наиболее существенные особенности схемы. Точная модель невозможна и нецелесообразна, так как приводит к резкому возрастанию вычислительных трудностей без существенного увеличения точности результатов.

Упрощение обычно состоит в том, что звенья с распределенными массами заменяются звеньями с массами, сосредоточенными в центрах тяжести звеньев; упругие звенья представляются в виде пружин, не

имеющих массы; звенья, масса которых незначительна, рассматриваются как абсолютно жесткие.

На рис. 6.18 представлены кинематическая и динамическая схема кулачкового механизма.

Рис.6.18. Динамическая модель кулачкового механизма

Здесь принята во внимание только упругость толкателя. Кулачок и его приводной вал считаются абсолютно жесткими. Масса деталей, связанных с толкателем, приведена к валу толкателя и представлена сосредоточенной массой m. Для упрощения считаем, что механизм нагружен чисто инерционной нагрузкой, т.е. нет силы полезного сопротивления.

Из представленной динамической схемы ясно, что перемещение верхнего конца толкателя y вследствие наличия пружины отличается от перемещения нижнего конца толкателя, движущегося по закону, определенному профилем кулачка.

Соотношение между перемещением s и y можно выяснить с помощью дифференциального уравнения движения массы m. Для составления этого уравнения воспользуемся принципом Даламбера. Масса находится в равновесии под действием двух сил - силы упругости пружины и силы инерции.

c(s–y)–my˝= 0, (6.5)

где s – перемещение нижнего конца; y – перемещение верхнего конца; с – коэффициент жесткости толкателя.

Коэффициент жесткости представляет отношение величины силы к величине деформации, вызванной этой силой. Он обычно определяется экспериментально.

Уравнение можно переписать в виде

y˝ + (c / m) y = (c / m) s (6.6)

или

s = y + (m / c) y˝.. (6. 7).

Уравнение (6.6) есть линейное дифференциальное уравнение с правой частью. Правая часть дифференциального уравнения условно понимается как возмущающая сила. В данном случае силы как таковой нет, но ее роль выполняет перемещение s, обеспечивающее так называемое кинематическое возбуждение. Если зависимость S (t) задана, то, решая дифференциальное уравнение, можно найти закон движения верхнего конца толкателя y (t). Разность s (t) – y (t) называется динамической ошибкой механизма. Она представляет интерес, например, при исследованиях вращающихся валов текстильных машин. Изменяя упругоинерционные характеристики механизма, можно добиться того, чтобы динамическая ошибка не превышала допустимой величины.

Уравнение (6.7) не является дифференциальным, так как неизвестная функция s (t) не входит под знаком производных. Это уравнение позволяет по заданному закону движения верхнего конца толкателя (y (t) и y˝ (t)) определить S (t), а затем найти необходимый профиль кулачка уже известными методами. Из уравнения (6.7) видно, что при абсолютно жестком толкателе (с = ∞) перемещения s и y совпадают.

Уравнение (6.7) используется для выбора закона движения толкателя, при котором отсутствуют мягкие и жесткие удары при упругом толкателе.

Продифференцируем по времени уравнение (6.7): s΄ = y΄ + (m / c) y˝΄ (6. 8)

Из уравнения (6.8) следует, что во избежание жестких ударов, определяемых скачком скорости, необходимо, чтобы y΄ и y ˝ были непрерывны на протяжении рабочего периода t_п и равны нулю на его границах. Установлено, что таким условиям удовлетворяют функции, являющиеся полиномами седьмой степени. Кулачки, спроектированные на основе таких законов называются полидинамическими.

С помощью уравнения (:6.6:) можно определить истинное движение верхнего конца толкателя.

Рис. 6.19. Графики движения толкателя

Рассмотрим это на примере центрального кулачкового механизма, у которого профиль кулачка определен на основании уравнения s = h (1 – cos φ)/2, график которого представлен на рис.6.19. Там же представлены графики скорости и ускорения. Как видно из этих графиков, нижний конец толкателя движется по закону косинусоидального ускорения.

Уравнение (6.6) в данном случае записывается в следующем виде:

y˝ + (c / m) y = (c / m) h (1 – cos φ) / 2.

Если ввести обозначения p² = c / m, (πt / t_п ) = φ, то уравнение запишется так:

y˝ + p² y = p² h (1 – cos (π t / t_п)./ 2.

Это уравнение представляет линейное неоднородное дифференциальное уравнение вида

y˝ + p² y = F (t),

общее решение которого, как известно, равно сумме решения соответствующего однородного уравнения y˝ + p² y = 0 и частного решения неоднородного уравнения.

Однородное уравнение есть уравнение свободных колебаний с циклической частотой p, решение которого

y₁ = A sin p t + B cos p t,

где А и В – некоторые постоянные коэффициенты.

Частным решением неоднородного урвнения является выражение

y₂ = h / 2 (1 – cos (π t / t_п)/ (1 - (π / p t_п)²)).

Общее решение уравнения

y = y₁ + y₂.

Постоянные А и В. находятся из начальных условий y = y΄ = 0 при t = 0.

После нахождения А и В и ряда преобразований получаем требуемое уравнение

y = h / 2 (n² – 1){ 1 – [ n² cos (π t / t_п) – cos (π t / t_п)]}, (6.9)

где n = t_п p / π = 2 t_п / T_c; T_c – период собственных колебаний.

Как видно из уравнения (6.9), график решения представляет сумму двух косинусоид с частотой p и p/n. Примерный вид графика y при n = 5 представлен на рис. 6.19 штриховой линией.

Оценка величины динамического эффекта, возникающего из-за упругости, производится с помощью коэффициента динамичности, представляющего отношение максимального ускорения при учете упругости к максимальному ускорению без учета упругости:

k = y˝_max ./ s˝_max.

Чтобы найти y˝_max, следует продифференцировать уравнение (6.9).

Для рассматриваемого закона косинусоидального ускорения коэффициент динамичности находится в пределах 2–3, стремясь при увеличении жесткости к 2. Для законов с мягкими ударами коэффициент динамичности оказывается больше 3.

Контрольные вопросы

1. В каких случаях применяются кулачковые механизмы?

2. Что такое фазовые углы кулачка?

3. Что такое мягкий удар и что такое жесткий удар? Как их избежать?

4. В чем состоит задача анализа кулачкового механизма?

5. Что такое угол давления и как он влияет на работу кулачкового механизма?

6. Что нужно сделать, чтобы при прочих равных условиях уменьшить угол давления в кулачковом механизме?

7. В чем состоит задача синтеза кулачкового механизма?

7.ОСНОВЫ ТЕОРИИ МАШИН – АВТОМАТОВ

7.1. Основные понятия теории машин – автоматов

Машина – автомат есть устройство, в котором все преобразования энергии, материалов и информации осуществляются без участия человека. Так, например, в станках – автоматах все рабочие и вспомогательные движения выполняются без участия человека. После выполнения совокупности движений устройство приходит в точно такое же состояние, в котором оно находилось перед их началом. Эта совокупность движений называется циклом. Машина – автомат выполняет цикл за циклом самостоятельно. Машина – полуавтомат требует вмешательства человека на границах цикла, например, для съема или установки детали.

Совокупность машин – автоматов, предназначенная для выполнения определенного технологического процесса, называется автоматической линией. Обычно кроме основного технологического оборудования в нее входят транспортные и другие вспомогательные устройства. Участие человека в работе автоматических линий состоит лишь в контроле за работой линий, наладке, устранению неисправностей.

Основная сфера применения автоматов и автоматических линий – массовое и крупносерийное производство, т.к. переналадка их на новое изделие требует материальных затрат и времени.

Машина – автомат состоит из одного или нескольких исполнительных органов, непосредственно воздействующих на обрабатываемый предмет, и блока управления, вырабатывающего управляющие воздействия на исполнительные органы. Источник, из которого блок управления черпает информацию, называется программой. Программа – это совокупность команд, которые должны быть выполнены для обеспечения требуемого технологического процесса. Программа разрабатывается заранее на основании проекта технологического процесса. Она физически реализуется на программоносителе.

7.2. Аналоговые системы управления

Существуют два принципиально различных способа задания программы: в аналоговом и в цифровом виде. Программа в аналоговом виде задается профилем кулачков, копиров, расстановкой упоров и конечных выключателей. Например, в приводе суппорта токарного станка – автомата имеется кулачковый механизм и зубчато – реечная передача, преобразующая поворот коромысла в поступательное движение суппорта (рис. 7.1).

На кулачке имеется участок быстрого подвода инструмента АВ и быстрого удаления СД, которые обычно выполняются по параболе, и участок рабочей подачи ВС. Так как обычно подача равномерная, участок ВС представляет спираль Архимеда.

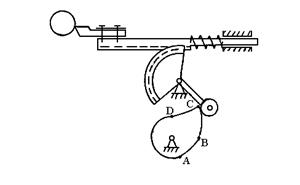
Рис. 7.1. Управление от кулачков

Кулачок является не только программоносителем аналогового типа, но и механизмом привода исполнительного органа, в данном случае – суппорта. Задаваясь различным профилем кулачка, можно получать различные законы движения исполнительного органа. Достоинства системы управления с кулачками – простота устройства, высокая точность. Недостатки – высокая стоимость изготовления кулачков и недостаточная долговечность, вследствие больших нагрузок на кулачок.

Другой способ задания программы в аналоговом виде – от копиров. Он обычно применяется при обработке деталей со сложным профилем типа кулачков, турбинных лопаток и т. д. На рис 7.2 представлена схема обработки фасонной цилиндрической поверхности по способу непосредственного копирования.

Рис.7.2.Управление от копиров

Стол фрезерного станка получает задающую подачу S_{з .} В результате обкатывания ролика – щупа по поверхности копира К возникает следящая подача S_с. Режущий инструмент полностью копирует движение щупа. Недостаток этого способа состоит в том, что для создания большого усилия резания пружина П должна быть достаточно мощной. А это вызывает большие нагрузки на щуп и копир, снижающие их долговечность. Этот недостаток устраняется, если применить следящий привод.

Принцип действия следящего привода поясняется схемой на рис. 7.3. Отличие от предыдущей схемы состоит в том, что усилие резания создается не пружиной, а силовым гидроцилиндром, питаемым от гидронасоса через сервоклапан.

Рис. 7.3. Следящий привод

Управление сервоклапаном осуществляется от копира посредством щупа. Сервоклапан выполнен так, что при одинаковых расстояниях фрезы и щупа от корпуса гидроцилиндра, пояски клапана перекрывают каналы, связывающие поршневую и штоковую полость силового гидроцилиндра. При появлении задающей подачи S_з щуп под действием копира перемещается вверх и сообщает штоковую полость с напорной магистралью, а поршневую – со сливной магистралью. Вследствие этого корпус гидроцилиндра, а вместе с ним и фреза, переместятся вверх на некоторую величину. Движение корпуса прекратится как только сервоклапан перекроет каналы, питающие гидроцилиндр. Процесс слежения всегда характеризуется некоторым запаздыванием подъема гидроцилиндра, вызывающим погрешность слежения. Надлежащим выбором параметров системы эту погрешность, а также колебания, возникающие из-за инерционности системы, можно свести к минимуму.

Рис. 7.4. Система управления по упорам

Наиболее простой является система управления по упорам. В качестве программоносителя выступает линейка или вращающийся барабан с закрепленными на них в определенных местах упорами. Эти упоры воздействуют на концевые выключатели, которые вырабатываю соответствующие сигналы и посылают их в систему управления. Например, с помощью упоров можно составить программу управления обработкой на токарном станке ступенчатого валика (рис. 7.4). Сигнал, вырабатываемый концевым выключателем, управляет поперечной подачей S_п.

Эта система широко применяется в автоматических линиях, в автооператорах, входит в состав систем блокировок и сигнализации различных устройств. Она конструктивно проста, универсальна, обеспечивает дистанционное управление, легко переналаживается.

7.3. Числовое программное управление

Система управления, работающие по программе, заданной в цифровом виде, называются системами с числовым программным управлением (ЧПУ). Они широко применяются в металлорежущих станках, в некотором технологическом оборудовании, в промышленных роботах. Основное достоинство этого способа – возможность быстрой подготовки и смены программы. Поэтому оборудование с ЧПУ удобно использовать при серийном и мелкосерийном производстве. Однако оно еще достаточно дорого.

При задании программы в цифровом виде программоносителем является в простейшем случае перфолента или магнитная лента.

Информация о величине требуемого перемещения каждого исполнительного органа задается в виде информационного числа Z.

Z = S / ∆S,

где S – величина требуемого перемещения,

∆S – величина единичного перемещения, шаг.

Для того чтобы реализовать шаговые перемещения, чаще всего используются шаговые электрические двигатели. Цепь питания этих двигателей включается импульсами, при каждом включении ротор поворачивается на определенный угловой шаг (рис. 7.5).

Рис. 7.5. Схема шагового электродвигателя

Полюса статора представляют электромагниты. Они разделены вдоль оси статора на секции I II III. Ротор также состоит из секций, которые представляют постоянные магниты с числом зубцов равным числу полюсов статора. Секции ротора повернуты друг относительно друга на одну треть полюсного угла α.

Если подать импульс постоянного тока на первую секцию, то вследствие притяжения разноименных полюсов они установятся друг против друга, а полюса второй и третьей секций расположатся со смещением на углы 1/3α и 2/3α. Если отключить первую секцию и включить вторую, то под действием электромагнитных сил полюса во второй секции установятся друг против друга, а ротор повернется на угол 1/3α. Затем, если выключить вторую и включить третью секцию, ротор повернется на угол 2/3α.

При переключении с первой секции на вторую и третью ротор вращается против часовой стрелки. При переключении с первой секции на третью, а затем вторую – по часовой стрелке. Скорость вращения ротора определяется частотой поступающих в двигатель импульсов тока, а общий угол поворота определяется количеством импульсов.

7.4. Система управления по времени

Графическое изображение рабочего цикла машины – автомата в масштабе времени дается цикловой диаграммой (циклограммой). Циклограммы могут быть линейными или круговыми. Циклограмма дает картину состояния исполнительных органов с их увязкой во времени. Циклограммой оговариваются не законы движения, а только сам факт движения и его направление. На линейных циклограммах движение обычно обозначается наклонными линиями, а покой – горизонтальными и поясняются соответствующими подписями. На циклограмме можно привести и другую полезную информацию

Циклограмма – это есть программа для системы управления по времени.

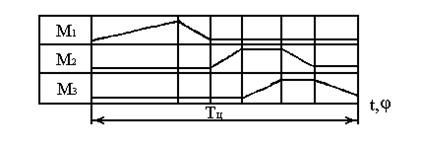
Рис. 7.6.Циклограмма машины-автомата

В качестве примера рассмотрим линейную циклограмму автомата для сверления отверстий (рис. 7.6). Механизм М1 выполняет сверление отверстий, механизм М2 разжимает крепление обработанной детали, механизм М3 снимает деталь и ставит новую. После этого начинается новый цикл.

Наиболее просто блок управления по времени реализуется с помощью кулачкового распределительного вала, вращающегося с постоянной скоростью. Полный поворот вала осуществляется за время Т_ц. Включение отдельных исполнительных органов осуществляется с помощью кулачков, повернутых друг относительно друга на углы пропорциональные соответствующим временным интервалам на циклограмме. В таком случае включение механизмов будет происходить в нужные моменты времени. Углы установки кулачков замеряются между начальными прямыми, т.е. прямыми, соответствующими началу подъема толкателя (рис. 7.7). Для кулачкового механизма с центральным толкателем и для одинаковых кулачковых механизмов с коромыслом углы установки кулачков совпадают с углами на циклограмме. Если используются неодинаковые кулачковые механизмы, углы установки определяются графическими построениями или аналитически.

Не нашли, что искали? Воспользуйтесь поиском: