Другие виды зацепления 6 страница

w= W₁ + W₂ . (8.11)

где Ω ₁ и Ω₂ – векторы относительнойскорости первого и второго движения, приведенные к неподвижному пространству.

Для абсолютного ускорения получено выражение

ε = E₁ + E₂ + W₁ Ω₂, (8.12)

где Е ₁ и Е ₂ - векторы относительного углового ускорения первого и второго движения, приведенные к неподвижному пространству; W ₁ – кососимметрическая матрица угловой скорости первого движения; W ₂ – вектор относительной угловой скорости второго движения. Векторы угловой скорости также приведены к неподвижному пространству.

Рис. 8.16. Сложение поворотов твердого тела

Из последней формулы следует, что если первое и второе вращения равномерны, движение относительно неподвижного пространства не будет равномерным движением, за исключением случае, когда векторы угловой скорости первого и второго движений параллельны. (В этом, в сущности, состоит объяснение гироскопического эффекта.)

Задача сложения поворотов возникает при анализе движения манипуляторов с шарнирным соединением звеньев руки. Такие манипуляторы имеют наибольшее распространение, несмотря на некоторое усложнение управления ими. Биологическим примером манипулятора с большим числом шарнирных соединений служит рука человека.

Приведенные выше формулы имеют универсальное применение во всех задачах механики сложного движения. В теоретической механике они обычно приводятся в несколько другой форме записи.

Матричная форма записи удобна тем, что она вносит ясность и единообразие при решении таких сложных задач как математическое описание механики сложного движения.

Единообразное представление важно с точки зрения организации вычислений при решении задач управления манипулятором. Перемножение матриц осуществляется по известному алгоритму. Прежде всего это имеет место при решении прямой задачи кинематики манипулятора, на базе которой строятся многие алгоритмы управления.

Прямая задача кинематики манипулятора состоит в следующем. Пусть задана схема шарнирного манипулятора (рис. 8.17), его обобщенные координаты, а также угловые скорости и ускорения в шарнирах. Требуется определить координаты, скорости и ускорения звеньев и характерных точек манипулятора.

Рис. 8.17. Системы координат шестизвенного манипулятора

Введем связанные со звеньями системы координат, как показано на рис. 8.17.

Зная обобщенные координаты звеньев, можно сформировать матрицы элементарных поворотов и затем перемножить их согласно выражению (8.3).

Для последнего звена шестизвенного манипулятора – схвата матрица ориентации получается из общего выражения для матрицы ориентации

τ₆=T₁T₂T₃T₄T₅T₆,

T_i – матрицы элементарных поворотов.

Для конкретной схемы манипулятора, представленной на рис. 8.17, с учетом вида матриц элементарных поворотов матрица ориентации последнего звена имеет вид

Y1X2X3Y4X5Y6.

Подставив сюда значения углов поворота в шарнирах, отсчитываемые от начальных положений соответствующих координатных осей звеньев, как это показано на рисунке, и произведя соответствующие вычисления, определим матрицу ориентации схвата.

Подчеркнем, что матрицы элементарных поворотов расставляются в порядке следования поворотов от неподвижного звена манипулятора. Соответствующие матрицы ориентации для остальных звеньев выглядят аналогичным образом, но несколько проще.

Для определения координат центров кинематических пар А_i воспользуемся формулой (8.8). Ее последовательное применение к соответствующим парам звеньев даст следующее выражение для определения координат некоторой точки S, принадлежащей схвату манипулятора:

R_S=R₁+t₂r₂+t₃r₃++t₄r₄++t₅r₅++t₆r₆.

Соответствующие выражения для остальных точек выглядят аналогично.

Угловые скорости и угловые ускорения звеньев находятся на основе последовательного применения формул (8.11) и (8.12), а линейные скорости и ускорения центров кинематических пар - на основе формул (8.9) и (8.10). Подробная запись этих выражений достаточно трудоемка, поэтому здесь она не приводится. Формулы рассчитаны на применение вычислительной техники.

8.8. Обратная задача кинематики манипулятора

Приведенные выше рекуррентные соотношения (8.8), (8.9), (8.10) позволяют определить положение, скорость и ускорение любых точек и звеньев манипулятора, если заданы обобщенные координаты и их производные по времени. Рассмотрим обратную задачу: определим обобщенные координаты, их скорость и ускорение, если задано движение исполнительного звена манипулятора — кисти, несущей захватное устройство или инструмент.

В общем случае положение исполнительного звена задается шестью эйлеровыми координатами: координатами полюса, в качестве которого может быть задан центр масс захватного устройства вместе с объектом манипулирования, и тремя углами, определяющими ориентацию захватного устройства связанной системы в неподвижном пространстве. Возникает шестимерная обратная задача по определению шести обобщенных координат.

Целесообразно максимально снизить размерность задачи. Для этого следует выяснить движение точек, максимально близкорасположенных к началу кинематической цепи. Такая возможность обычно существует благодаря тому, что присоединение кисти робота к несущей руке можно смоделировать сферической кинематической парой. Тогда, рассматривая кисть как твердое тело, осуществляющее предписанное пространственное движение, по известным формулам кинематики определим движение центра сферической пары. Задача стала трехмерной: требуется определить три обобщенные координаты для трехзвенной кинематической цепи позиционирующих движений по заданным координатам исполнительной точки. Для этого необходимо решить векторное уравнение

F(q₁,q₂,q₃) = R_A⁰ – R_A (q₁, q₂, q₃) = 0, (8.13)

где F = [ f₁ (q₁ ), f₂ (q₂), f₃ (q₃) ], R _A⁰ — заданный радиус-вектор точки; R _A— вектор-функция положения точки, найденная из решения прямой задачи.

Для численного решения уравнения (8.13) можно применить метод Ньютона. Предположим, что найдено p-тое приближение искомых координат q^p = [ q₁^p, q₂^p, q₃^p ]. Тогда следующее приближение можно представить в виде

q^{(p+ 1)} = q^(p) + ε,

где ε — поправка.

Поправка ε находится из линейной системы уравнений

Wε = - R _A (q^(p)), (3.14)

где W — матрица Якоби системы скалярных функций :

Матрица Якоби вычисляется при значениях q_i, соответствующих p-му приближению. При исследовании движения на границах рабочей зоны могут возникнуть затруднения в связи с вырождением матрицы W, а значит, и невозможностью решения линейного уравнения (8.14).

Для ортогональных манипуляторов существует возможность составления алгоритма решения обратной задачи, который более эффективен, чем метод последовательных приближений

Решение обратной задачи кинематики для манипуляторов с прямоугольной, цилиндрической и сферической системами координат не вызывает затруднений. Анализируя схемы на рис. 8.5, 8.6, 8.7, можно вычислить обобщенные координаты по заданному положению исполнительной точки S.

Для манипулятора с прямоугольной системой

с цилиндрической системой

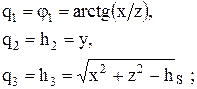
со сферической системой

Дифференцируя эти соотношения можно получить формулы для скорос-

тей и ускорений.

Для манипулятора с шарнирной схемой задача решается несколько

сложнее. (Подробнее можно прочитать в книге «Механика промыш-

ленных роботов и манипуляторов с электроприводом» Л.А. Борисенко,

А.В. Самойленко. – Мн. 1992 г.)

8.9. Предварительный силовой расчёт манипулятора

Предварительный расчёт манипулятора можно вести по упрощенной схеме кинетостатического расчёта, считая звенья геометрическими с сосредоточенными точечными массами, помещёнными в центрах их масс.

На этапе предварительного расчёта манипулятора производится ориентировочный расчёт мощности двигателя, определяется быстродействие манипулятора. При расчёте мощности двигателя учитываются такие параметры, как масса переносимого груза, максимальный радиус вылета руки (для телескопической руки), предельные перемещения груза по координатам, номинальная скорость движения. Расчёт ведется для периода неустановившегося движения, каким является период пуска. Рассмотрим, например, вращательное движение модуля поворота руки шарнирного манипулятора, схема которого представлена на рис.8.23.

Рис.8.23. Манипулятор со статически уравновешенной рукой

В период пуска момент двигателя складывается из статического момента, создаваемого весом руки, рабочего органа и переносимого груза, и динамического момента, связанного с неравномерностью движения по координате φ: М =Мст+ Мдин.

В случае статически уравновешенной руки Мст определяется только весом груза и радиусом размещения его относительно шарнира А. Вопрос уравновешивания руки имеет важное практическое значение как для облегчения управления при обучении, так и для энергетики манипулятора.

Известно, что для статической уравновешенности необходимо, чтобы при изменении положения системы центр масс оставался неподвижным. Эта задача для звена, совершающего вращательное движение, решается путём добавления к нему дополнительной массы (так называемого дебаланса) или таким распределением массы звена, чтобы центр его масс оказался в центре шарнира. Этот приём непригоден при телескопической руке, так как из-за движения в поступательной паре происходит изменение положения центра масс и, следовательно, необходимо непрерывно корректировать положение дебаланса, что трудновыполнимо. С целью статического уравновешивания руки манипулятора наиболее массивные его части, к которым относятся двигатели с редукторами, располагаются за шарниром, как это показано на рис.8.23, с таким расчётом, чтобы центр масс оказался в точке А. Перераспределение веса может увеличить динамическую неуравновешенность. Поэтому для статического уравновешивания руки применяются также специальные пружинные или пневматические уравновешивающие устройства.

Даже при полной статической уравновешенности руки остаётся статический момент от неуравновешенной массы переносимого груза. С учётом остаточной статической неуравновешенности

Мст= kCmgrScosα,

где kC – коэффициент статической неуравновешенности руки, согласно практическим данным, принимается 1,5; m – масса груза; rS – постоянный радиус центра масс груза; α – угол наклона руки к горизонту.

Динамический момент Мдин, преодолеваемый двигателем в случае вращательного движения вокруг оси:

Мдин= –Jε,

где J – момент инерции руки совместно с переносимым грузом относительно центра вращения; ε – угловое ускорение.

Эту же формулу можно представить в виде

Мдин= kДmgrSε,

где kД– коэффициент динамической неуравновешенности руки, учитывающий момент инерции вращающихся частей привода и самой руки без груза; по данным для существующих конструкций роботов типа обычно kД = 1,8–2,3.

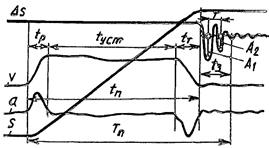
Рис. 8.24.Осцилограмма параметров переносного движения руки

Динамический момент зависит в первую очередь от углового ускорения ε. Выбор допустимого значения е следует производить на основании имеющегося опыта эксплуатации роботов. На рис. 8.24 представлена осциллограмма переносного движения руки робота. Она включает период разгона tр, установившегося движения tуст, торможения tт. На рисунке 8/24 v – скорость движения, a – ускорение, S – перемещение, ∆S – малые упругие колебания руки, Тп – полное время движения, включающее время успокоения рабочего органа.

Закон изменения скорости обычно принимается трапецеидальным, тогда разгон и замедление происходят с постоянным ускорением. Длины пути разгона и торможения принимают обычно равными и составляющими некоторую часть общего перемещения:

φр= φт= kφφ,

где k_φ – коэффициент быстродействия.

Табл.8.1. Предельные параметры перемещений руки человека

Чем меньше kφ, тем быстрее нарастает скорость, а следовательно, и увеличиваются динамические нагрузки на звенья. С целью ограничения максимальных ускорений до значений ε = 10–20 рад/с2, что для манипулятора средних размеров соответствует линейным ускорениям 5–10 м/с2, при ориентировочном расчёте можно принимать kφ = 0,1–0,2.

Динамическое совершенство руки манипулятора ещё очень невысокое. В табл.8.1 приведены среднестатистические предельные возможности перемещения руки человека.

Путь разгона для принятого закона равноускоренного движения связан с продолжительностью движения и угловой скоростью зависимостями

φр= ε tр2/2, φр= ω2 / (2ε).

Увеличение быстродействия манипулятора приводит к росту динамической составляющей момента, поэтому возникает задача оптимизации параметров быстродействия.

Мощность привода вращательного движения передачи двигатель – исполнительный орган определяется по формуле

N = Mω / η,

где η – общий КПД передачи; в зависимости от вида редуктора и значения передаточного отношения η = 0,3 – 0,8.

Двигатель должен обладать достаточной мощностью для обеспечения надёжной работы в переходных режимах.

Контрольные вопросы

1. Что понимается под словом робот в широком смысле слова?

2. Как классифицируются манипуляционные роботы?

3. Начертите функциональную схему автоматического робота.

4. Что такое промышленный робот?

5. По каким признакам квалифицируются промышленные роботы?

6. Охарактеризуйте назначение глобального, регионального и локального движения робота.

7. Сколько степеней свободы должен иметь полный манипулятор?

8. Как реализуется кинематическая цепь региональных движений?

9. Дайте сравнительную оценку манипуляторов с прямоугольной, цилиндрической, сферической системами координат.

10. Нарисуйте схему шарнирного робота.

11. Как обычно осуществляется кинематическая цепь ориентирующих движений?

12. Как задается ориентация тела в пространстве?

13. Запишите матрицы элементарных поворотов вокруг осей x, y, z.

14. В чем состоит прямая задача кинематики манипулятора?

15. В чем состоит обратная задача кинематики манипулятора?

16. В чем состоит предварительный силовой расчет манипулятора?

17. Как определить мощность привода для вращательного движения уравновешенной руки манипулятора?

ОГЛАВЛЕНИЕ

Предисловие 3

Введение 4

1. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА МЕХАНИЗМОВ.

1.1. Основные понятия курса теории механизмов, машин и

манипуляторов 11

1.1. Виды и классификация кинематических пар 12

1.2. Кинематическая цепь. Кинематическое соединение 14

1.3. Число степеней свободы механизма 15

1.4. Классификация плоских механизмов с низшими парами 17

1.5. Разновидности четырехзвенных рычажных механизмов 18

1.6. Зубчатые, кулачковые, фрикционные механизмы 20

2. КИНЕМАТИКА МЕХАНИЗМОВ

2.1. Задачи кинематики механизмов 23

2.2. План положений механизма 23

2.3. Основные кинематические соотношения 24

2.4. Метод планов скоростей и ускорений

План скоростей шарнирного четырехзвенника 27 2.5. План ускорений шарнирного четырехзвенника 29

2.6. Планы скоростей и ускорений кулисного механизма 30

2.7. Метод кинематических диаграмм 35

2.8. Аналитический метод исследования

открытой кинематической цепи 37

2.9. Кинематическое исследование рычажных механизмов

с замкнутыми цепями 38

2.10. Обобщенные координаты, уравнения связей,

математическая модель пространственной кинематической

цепи 43

3. ДИНАМИЧЕСКИЙ АНАЛИЗ МАШИН И МЕХАНИЗМОВ

3.1. Задачи динамики машин 46

3.2. Классификация сил в механизмах 46

3.3. Сила инерции 47

3.4. Силы инерции в поступательном, вращательном и сложном движении 52

3.5. Силовое исследование механизмов методами кинетостатики 54

3.6. Условие статической определимости кинематической цепи 55

3.7. Метод планов сил 56

3.8. Метод рычага Жуковского 58

3.9. Аналитический метод силового исследования 59

3.10. Задача уравновешивания ротора 59

3.11. Статическая неуравновешенность ротора 60

3.12. Моментная неуравновешенность ротора 61

3.13. Полное уравновешивание ротора с известным

расположением масс 62

3.14. Балансировка на машинах 63

3.15. Уравновешивание механизмов 63

3.16. Силы трения в механизмах. Законы трения 64

3.17. Трение в поступательной паре 65

3.18. Трение во вращательной паре 67

3.19. Трение в высших парах 68

3.20. Динамический анализ механизмов. Приведение сил и масс 68

3.21. Уравнение движения машины в дифференциальной форме 70

3.22. Пример динамического исследования колодочного тормоза 71

3.23. Численное решение дифференциального уравнения 71

3.24. Периоды работы машины 72

3.25. Регулирование неравномерности хода машины 73

3.26. Автоматические регуляторы скорости 75

3.27. Одномассовая упругая модель механизма 76

3.28. Характеристики упругих звеньев 80

4. СИНТЕЗ РЫЧАЖНЫХ МЕХАНИЗМОВ

4.1. Задачи синтеза механизмов 85

4.2. Структурный синтез рычажных механизмов 85

4.3. Синтез четырехзвенных механизмов

по заданным положениям звеньев 87

4.4. Синтез механизмов по коэффициенту производительности 88

4.5. Учет угла давления при синтезе механизмов 89

4.6. Направляющие механизмы. Механизмы с выстоями 90

4.7. Шаговые механизмы. Мальтийские механизмы 91

4.8. Механизмы пантографов 92

4.9. Синтез механизмов методами оптимизации 93

4.10. Синтез сферических рычажных механизмов 95

5. СИНТЕЗ ЗУБЧАТЫХ МЕХАНИЗМОВ

5.1. Классификация зубчатых механизмов 98

5.2. Понятие о центроидных механизмах 99

5.3. Основной закон зацепления 100

5.4. Эвольвента окружности, построение и свойства 101

5.5. Уравнение эвольвенты в полярных координатах 102

5.6. Эвольвентное зацепление 103

5.7. Изготовление зубчатых колес 107

5.8. Исходный контур 104

5.9. Элементы нулевого зубчатого колеса 105

5.10. Нарезание зубчатых колес со смещением 106

5.11. Влияние смещения на профиль зуба 107

5.12. Подрезание, интерференция, заострение 107

5.13. Построение картины зацепления 109

5.14. Коэффициент перекрытия 109

5.15. Толщина зуба по окружности произвольного радиуса 111

5.16. Геометрический расчет зубчатой передачи 111

5.17. Блокирующие контуры 112

5.18. Косозубые колеса 113

5.19. Другие виды зацепления 114

5.20. Пространственные зубчатые передачи 115

5.21. Передаточное отношение и передаточное число 117

5.22. Расчет рядовой коробки передач 118

5.23. Планетарные зубчатые механизмы 119

5.24. Аналитический метод определения передаточного

отношения и угловых скоростей планетарных механизмов 120

5.25. Кинематический анализ автомобильного дифференциала 121

5.26. Замкнутые дифференциальные механизмы 122

5.27. Дифференциальные коробки передач 123

5.28. Графический метод анализа планетарных механизмов 123

5.29. Условия соосности, соседства, сборки планетарных механизмов 124

5.30. Пример синтеза планетарного механизма 126

5.31. Волновая передача 127

5.32. Планетарные механизмы робототехнического назначения 128

6. СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ

6.1. Виды кулачковых механизмов 133

6.2. Заменяющие механизмы 134

6.3. Элементы профиля кулачка 135

6.4. Выбор закона движения толкателя 136

6.5 Изготовление кулачков 137

6.6. Анализ кулачковых механизмов 137

6.7 Угол давления и его связь с размерами кулачка 138

6.8 Определение основных размеров кулачкового

механизма с коромыслом 140

6.9 Определение размеров кулачкового механизма

с тарельчатым толкателем 142

6.10 Построение профиля кулачка по заданному

закону движения толкателя 144

6.11 Динамический анализ кулачковых механизмов 147

7 ОСНОВЫ ТЕОРИИ МАШИН-АВТОМАТОВ

7.1. Основные понятия теории машин-автоматов 152

7.2. Аналоговые системы управления 152

7.3. Числовое программное управление 155

7.4. Система управления по времени 156

7.5. Основы синтеза логических систем управления 157

7.6. Синтез избирательной системы управления 159

8. РОБОТЫ И МАНИПУЛЯТОРЫ

8.1. Общие сведения о роботах и манипуляторах 162

8.2. История развития робототехники 163

8.3. Классификация роботов 164

8.4. Промышленные роботы 166

8.5. Структура и геометрические характеристики манипуляторов 170

8.6. Задание ориентации твердого тела 175

8.7. Кинематика манипулятора 179

8.8. Обратная задача кинематики манипулятора 184

8.9. Предварительный силовой расчет манипулятора 185

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ

Активная линия зацепления 109

Анкерный механизм 91

Автоматизированный робот 165

Автоматическая линия 152

Асинхронный кардан 96

Блок управления 152

Блок-схема системы управления 160

Биотехнический робот 164

Входное звено 12 Выходное звено 12

Вариатор 21

Вращательное движение 25

Волновая передача 21

Волновая зубчатая передача 127

Высшие пары 13

Головка зуба 104

Грейферный механизм 91

Глобальные движения 170

Делительная прямая 104

Делительная окружность 105

Движущая сила 46

Динамическая эквивалентность 68

Динамика механизмов 46

Деталь 11

Двухкривошипный механизм 18

Дифференциал 12

Двухкоромысловый механизм 18

Диада 16

Диалоговое управление 165

Заострение зуба 108

Звено приведения 68

Замкнутая кинематическая цепь 14

Зубчатый механизм 20

Зубчато-рычажный механизм 20

Закон Ньютона 48

Зубчатый ряд 20

Зона обслуживания 175

Зубчатое колесо 98

Зубчатая передача 98

Зубчатый механизм 98

Избыточные связи 16

Инволюта 102

Исходный контур 104

Интерференция 108

Информационная машина 11

Инерциальная система отсчета 47

Исплнительное устройство 175

Исполнительный орган 152

Информационная система 166

Исполнительная система 166

Интеллектный робот 167

Кинематическая схема механизма 12

Конструктивная схема механизма 12

Кинематическое соединение 14

Класс группы 18 Класс механизма 18

Кисть робота 174

Коэффициент смещения 106

Кинематическая пара 12

Кривошипно – коромысловый механизм 18

Кривошип 18 Коромысло 18

Крестовое соединение 15

Кулисный механизм 17

Кривошипно-ползунный механизм 17

Камень 17

Крестовая муфта 17

Кулачковый механизм 20

Коромысло 20

Кинематика 23

Круговое поступательное движение 25

Кинематическая теорема Кориолиса 48

Крайнее положение механизма 88

Коэффициент производительности 88

Кулачок 133

Командное управление 164

Копирующий робот 164

Кардан 95

Коэффициент перекрытия 109

Локальные движения 170

Мультипликатор 117

Мертвое положение 86

Механизм косой шайбы 96

Механизм косой шайбы 96

Моментная неуравновешенность 61

Машина 11

Машина-автомат 11

Манипулятор 11

Механизм 14

Метод преобразования координат 37

Механизм 1-го класса 16

Механизм с качающейся кулисой 17

Механизм Ольдгейма 17

Механизм с вращающейся кулисой 17

Метод преобразования координат 23

Метод кинематических диаграмм 35

Механизм 11

Масштабный коэффициент 23

Метод засечек 23

Метод кинетостатики 54

Механизм свободного хода 91

Мальтийский механизм 91

Матрица Якоби 184

Манипулятор 166

Машина-автомат 152

Редуктор 117 Передаточное отношение 117

Передаточное число 117

Условие соосности 125 условие сборки 125

Условие соседства 125

Эвольвента 101 Угол профиля эвольвенты 102

Эвольвентная функция 102

Начальная окружность 103 Способ копирования 103

Способ обкатки 103

Теоретический исходный контур 104

Шаг рейки 104 Толщина зуба 104

Ширина впадины 104

Начальная прямая 104

Ножка зуба 104 Производящий исходный контур 104

Смещение 106

Угол перекрытия 110

Одномассовая динамическая

модель механизма 68

Существование кривошипа 86 Теорема Грасгофа 86

Направляющие механизмы 90

Прямой ключ Гука 96 Синхронный кардан 96 Универсальный кардан Рзеппа 96

Уравновешивающая сила 56 Условие статической

определимости системы 55

Статическая неуравновешенность 60

Самоторможение 66

Прямая задача динамики 46 Обратная задача динамики 46

Энергетическая машина 11

Технологическая машина 11 Транспортная машина 11

Звено 11

Стойка 11

Промежуточное звено 12

Элемент кинематической пары 12

Структурная схема механизма 12

Обобщенная координата 14 Кинематическая цепь 14

Плоская кинематическая цепь 14

Пространственная кинематическая цепь 14

Не нашли, что искали? Воспользуйтесь поиском: