Другие виды зацепления 5 страница

Термин «поколение» надо понимать лишь как степень развития технических возможностей. Рассматриваемые разновидности роботов не вытесняют друг друга, каждая из них будет существовать наряду с другими при постепенном совершенствовании их элементной базы.

По степени специализации ПР разделяются на специальные, специализированные (целевые) и многоцелевые. Специальным называется робот, предназначенный для выполнения определенных технологических операций или обслуживания конкретной модели технологического оборудования.

Специализированные роботы служат для выполнения технологических операций одного вида (сварка, окраска, сборка и т.п.) или для обслуживания определенной группы моделей технологического оборудования (например, группы моделей станков с горизонтальной осью шпинделя).

Многоцелевые роботы предназначены для выполнения различных основных и вспомогательных технологических операций. Они конструктивно не зависят от обслуживаемого оборудования и характеризуются разнотипностью совершаемых движений.

По выполняемой функции ПР подразделяются на вспомогательные, технологические и универсальные. Вспомогательные роботы выполняют операции типа "взять—перенести". Технологические роботы используются в качестве производящих или обрабатывающих машин на таких операциях, как гибка, сварка, сборка, окраска, контроль и т.п. Универсальными называются роботы, совмещающие функции вспомогательного и технологического роботов.

Под грузоподъемностью ПР понимается наибольшая масса объектов манипулирования (включая массу рабочего органа), которые могут перемещаться рукой робота при заданных условиях (при максимальной или минимальной скорости, при максимальном вылете руки и т.п.). По грузоподъемности ПР делятся на сверхлегкие (до 1 кг), легкие (до 10 кг), средние (до 200 кг), тяжелые (до 1000 кг), сверхтяжелые (свыше 1000 кг).

Рабочая зона манипулятора — это пространство, в котором находится его рабочий орган при всех возможных положениях манипулятора. Рабочая зона характеризуется объемом. По объему рабочей зоны ПР делятся на микророботы, выполняющие особо точные операции с весьма мелкими деталями (например, при производстве изделий микроэлектроники), мини-роботы для точных операций с мелкими деталями (например, при производстве часовых механизмов), малые роботы, предназначенные, например, для операций холодной штамповки, средние роботы для операций, которые рабочие выполняют стоя, крупногабаритные роботы для выполнения операций, превышающих физические возможности человека, и, наконец, мобильные роботы, перемещающиеся по рельсовому пути, монорельсу или как-нибудь иначе.

По числу степеней подвижности ПР подразделяются на роботы с двумя, тремя, четырьмя степенями подвижности и роботы со степенями подвижности более четырех.

По форме рабочей зоны ПР делятся на прямоугольные, цилиндрические, сферические, ангулярные (антропоморфные) и комбинированные (рис.8.3). Это определяется системой координат, с которой совпадает система обобщенных координат манипулятора.

По виду привода ПР подразделяются на электромеханические, гидравлические, пневматические, роботы с комбинированным приводом.

Под программным управлением понимается автоматическое управление исполнительным устройством промышленного робота по заранее введенной управляющей программе. По типу системы управления ПР подразделяются на роботы с позиционным управлением и с контурным управлением.

а

Рис. 8.3 - Схемы промышленных роботов:

а — прямоугольная; б — цилиндрическая; в — сферическая;

г — антропоморфная; д — комбинированная

Под позиционным управлением понимается программное управление ПР, при котором движение рабочего органа происходит по заданным точкам позиционирования без контроля траектории движения между ними.

Частным случаем позиционного управления является цикловое управление, при котором точки позиционирования задаются при помощи жестких упоров. При цикловом управлении программируется только последовательность движений.

Под контурным управлением понимается управление ПР, при котором движение рабочего органа происходит по заданной траектории с определенной скоростью.

При позиционной системе управления сводится к минимуму отклонение от требуемого положения при подходе к конечным точкам, но не контролируется движение между этими точками, а также не контролируется сочетание движений по отдельным степеням подвижности. Такое перемещение приемлемо для операций загрузки—выгрузки металлорежущих станков, точечной сварки, но не пригодно для операций окраски или дуговой сварки.

Системы контурного управления обеспечивают движение по непрерывным траекториям с заданной скоростью. Для этого необходимо осуществить скоординированное управление движением по всем степеням подвижности. Обычно используется способ контурного управления с интерполятором. Это по существу позиционное управление, дополненное специальным вычислительным блоком — интерполятором, который по определенному алгоритму осуществляет расчет отрезков траекторий между заданными программными точками.

8.5. Структура и геометрические характеристики манипуляторов

Движения, совершаемые человеком и воспроизводимые роботом, можно разделить на три класса: глобальные, региональные, локальные.

Глобальные движения — это перемещения на расстояния, превышающие размеры робота. Робот, совершающий глобальные движения, называется мобильным, а не совершающий — стационарным. Глобальные движения совершает робот, перемещаясь по подвесному монорельсу. Так, например, работают роботы, обслуживающие группу металлорежущих станков, установленных на одной линии. У большинства роботов глобальные движения отсутствуют.

Движения, совершаемые рукой робота в пределах его рабочей зоны и соизмеримые с его габаритами, называются региональными. Их также называют переносными, так как они обеспечивают перенос объекта в требуемую точку. Эти движения соответствуют движениям, реализуемым плечом и предплечьем руки человека.

Локальные движения — это перемещения рабочего органа в малой зоне. Они соответствуют движениям кисти руки. Основное назначение этих движений — ориентирование объекта манипулирования в данной точке рабочего пространства, поэтому их также называют ориентирующими.

С введением понятий регионального и локального движений кинематическую цепь стационарного манипулятора можно расчленить на две функциональные части, отвечающие за эти движения, — переносную и ориентирующую и соответственно выделить переносные и ориентирующие степени подвижности, обеспечивающие эти движения.

Как известно из механики, положение тела в пространстве определяется шестью обобщенными координатами. Произвольное движение твердого тела может быть разложено на поступательное перемещение, связанное с некоторой произвольно выбранной точкой, и вращение относительно этой точки. Соответственно из шести независимых обобщенных координат, описывающих движение твердого тела, три координаты задают перемещение некоторой фиксированной точки тела в пространстве, а три характеризуют его вращение. Пространственный манипулятор в общем случае должен иметь шесть степеней подвижности: три для отработки региональных (переносных) движений и три — для локальных (ориентирующих).

В том случае, когда приходится манипулировать с несвободными предметами, на которые наложены дополнительные связи, может оказаться, что указанных степеней подвижности мало. Так, например, для того чтобы наживить и завинтить гайку, поднять с пола ящик стола для установки его в направляющие стола, достаточно иметь манипулятор с шестью степенями подвижности. Однако без седьмого движения, винтового или прямолинейно-поступательного вдоль направляющих, нельзя навинтить гайку и задвинуть ящик в стол иначе, как используя сложную комбинацию движений.

Число степеней подвижности более шести может оказаться необходимым при выполнении сложных работ, связанных с дополнительными ограничениями на перемещение звеньев манипулятора при работе в стесненном пространстве. Увеличение числа степеней подвижности наделяет манипулятор ценным свойством избыточности, однако это усложняет его и повышает его стоимость.

Рис. 8.4 - Структурные схемы ортогональных манипуляторов

Для промышленных роботов, работающих в организованном рабочем пространстве, где рабочие зоны упорядочены и, как правило, лежат в горизонтальных и вертикальных плоскостях, при выполнении рабочих операций обычно оказывается достаточным 4—5 степеней (3 переносных и 1—2 ориентирующих). Простейшие не перепрограммируемые роботы, называемые автооператорами, могут иметь 1 —2 степени подвижности.

Кинематическая цепь региональных движений обычно осуществляется с использованием кинематических пар пятого класса (вращательных, поступательных соединений) и содержит три звена. В таком случае возможны следующие последовательности расположения кинематических пар: ВВВ, ВВП, ВПВ, ПВВ, ППВ, ПВП, ВПП, ППП. Оси соседних кинематических пар могут иметь самое различное относительное расположение, однако получили распространение манипуляторы с коллинеарными или ортогональными осями (их называют ортогональными манипуляторами).

Схемы манипуляторов весьма разнообразны (рис. 8.4).

Из приведенных на рис. 8.4 схем наиболее распространены структурные схемы типа BBB₁, ВВП₂, ВПП, ППП. Одной из простейших является схема ППП (рис. 8.5) с прямоугольной системой координат, форма ее рабочей зоны — параллелепипед. Такая схема наиболее удобна для выполнения прямолинейных движении. При этом максимально упрощено программирование робота, так как нет необходимости пересчета декартовых координат в обобщенные координаты (q₁=h₁=z_s, q₂=h₂=y_s, q₃=h₃+h_s=x_s). Эта система применяется в станках с ЧПУ, которые также являются своеобразными манипуляторами, и в сборочных роботах. Недостатки этого исполнения — увеличение габаритов устройства, сравнительно низкое быстродействие, сложность изготовления направляющих.

В настоящее время наибольшее распространение получили роботы со схемой ВПП — роботы с цилиндрической системой координат (рис. 8.6). Их рабочее пространство имеет форму цилиндра или его части. Рука может осуществлять движение по горизонтали и вертикали и поворот вокруг оси колонны. Робот с таким исполнением компактен при большом обслуживаемом объеме, относительно прост при программировании. Его недостатком является наличие мертвого необслуживаемого пространства у основания. Такую схему обычно имеют транспортные роботы.

Рис. 8.5 - Манипулятор с прямоугольной системой координат

Манипулятор исполнения ВВП₂ имеет сферическую систему координат, его рабочее пространство — сферический сегмент (рис. 8.7). Роботы с такой системой координат сложнее, чем с цилиндрической системой, но компактнее, обслуживают больший объем, включая зоны, выходящие за их габариты сверху и снизу. Роботы этого исполнения имеют повышенную жесткость, что позволяет их использовать при больших нагрузках, например при автоматизации точечной сварки и т.п.

Манипулятор исполнения ВВВ₁ со сложной сферической системой координат (рис. 8.8) называется ангулярным, шарнирным или антропоморфным.

Рис. 8.6. Манипулятор с цилиндрическойсхемой и его обобщенные координаты

Основное достоинство такого манипулятора — значительно меньшие габариты, чем у манипулятора с поступательными парами, при большой зоне обслуживания. Он может применяться в стесненной зоне обслуживания. Такие манипуляторы обычно хорошо уравновешены и поэтому часто используются, когда программирование осуществляется методом обучения рукой человека на операциях окраски, нанесения защитных покрытий и т.п.

Каждая из рассмотренных схем обладает определенными достоинствами и недостатками, поэтому выбор схемы является компромиссным решением и ведется с учетом предъявляемых к данному роботу требований. При выборе схем надо принимать во внимание не только их функциональные возможности, но и упрощение конструкции, технологичность ее изготовления, стоимость. При решении этих вопросов следует руководствоваться уже накопленным опытом проектирования роботов.

Основные технические характеристики робота — грузоподъемность, размеры зоны обслуживания, быстродействие, точность — тесно связаны между собой и с его компоновкой. Улучшение одних характеристик можно получить только за счет ухудшения других. Так, в частности, большая грузоподъемность несовместима с большим размером зоны обслуживания, большая скорость — с высокой точностью. Отсюда следует, что нет такой схемы робота, которая была бы оптимальной во всех случаях.

Рис. 8.7. Манипулятор со сферической схемой и его обобщенные координаты

Кинематическая цепь, реализующая локальные движения, называется кистью робота, поскольку она выполняет функции, аналогичные кисти руки человека. Назначение кисти — ориентирующие движения. Из механики известно, что произвольную ориентацию твердому телу можно задать путем трех последовательных плоских поворотов, производимых относительно несовпадающих осей, в частности взаимно ортогональных, связанных с телом.

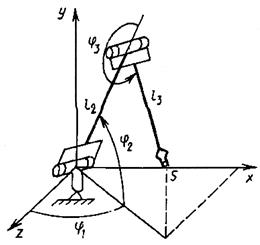
Рис. 8.8. Манипулятор с антропоморфной схемой (шарнирный манипулятор) и его обобщенные координаты

Механической моделью, осуществляющей физическую реализацию таких движений, служит карданов подвес, представляющий трехзвенную кинематическую цепь с одними вращательными парами, причем оси пар пересекаются в одной точке. При этом движение выходного звена будет сферическим с центром в точке пересечения осей. Оно является композицией трех движений (рис. 8.9): прецессии (движения тела 1 по отношению к телу 0), нутации (движения тела 2 по отношению к телу 1), чистого вращения или ротации (движение тела 3 по отношению к телу 2).

Рис. 8.9. Устройство для ориентации кисти на основе карданова подвеса

Для удержания объекта манипулирования кисть снабжается захватным устройством. Назначение переносных и ориентирующих движений — поместить захватное устройство в любую точку рабочей зоны. Однако не всякая точка рабочей зоны манипулятора в равной мере доступна захватному устройству, так как на его положение накладываются ограничения, связанные с конструкцией кинематических пар и длиной звеньев. Эти ограничения не позволяют подводить захват (схват) к данной точке под любым желаемым углом.

Рис. 8.10. Зона обслуживания манипулятора

Углом сервиса называется телесный угол, в пределах которого может находиться продольная ось захвата в том случае, если его центр находится в данной точке пространства. Рассмотрим манипулятор, схема которого приведена на рис. 8.10. Площадь F сферической поверхности с центром в точке 5 и радиусом r = SA равна 4pr², где 4тс — телесный угол для сферы. Ось захвата манипулятора CBAS может занимать положение внутри некоторого шарового сектора, являющегося лишь частью сферы, определяя тем самым сферическую поверхность площади Ф_i = q_i r₂, где q_i — угол сервиса, причем q_i < 4π. Отношение x_i = Ф_i/F = q_i/(4p) называется коэффициентом сервиса для манипулятора в данной точке. На границе рабочего пространства этот угол, очевидно, равен нулю. Максимальное значение коэффициента сервиса равно единице. В этом случае захват совершает полное сферическое движение вокруг данной точки. Интегральной оценкой совершенства манипулятора является полный коэффициент сервиса, вычисляемый по формуле

где — элемент рабочего объема V.

ГОСТ 25686—85 вводит ряд определений, касающихся роботов и их геометрических характеристик.

Исполнительным устройством называется устройство, выполняющее все двигательные функции робота.

Рабочий орган — составная часть исполнительного устройства для непосредственного выполнения технологических операций и (или) вспомогательных переходов.

Рабочее пространство манипулятора — часть физического пространства, в котором может находиться исполнительное устройство при функционировании манипулятора.

Рабочая зона — пространство, в котором может находиться рабочий орган.

Зона обслуживания — пространство, в котором рабочий орган выполняет свои функции в соответствии с назначением.

Погрешность позиционирования рабочего органа манипулятора—отклонение положения рабочего органа от заданного управляющей программой.

Погрешность отработки траектории — отклонение траектории от заданной.

8.6. Задание ориентации твердого тела

Рассмотрим твердое тело в трехмерном векторном пространстве. Пусть хуz, — неподвижная система координат, а Е — соответствующее ей векторное пространство. Система координат ξης — подвижная, жестко скрепленная с телом, а I - соответствующее ей векторное пространство (рис. 8.11).

Рис.8.11. Задание ориентации системы координат твердого тела с помощью направляющих косинусов

Оператором преобразования координат от пространства I к пространству E, соответствующим данной ориентации твердого тела, назовем оператор τ, осуществляющий следующее преобразование векторов:

R = τ r. (8.1)

Вектор r, т.е. радиус-вектор некоторой точки тела, рассматривается в пространствe I, ему соответствует вектор R, с которым он "совпадает" в пространстве E.

Равенство (8.1) можно записать иначе в развернутой матричной записи, имея в виду, что, r = [ ξ,η,ς ], R = [ x,y,z ] — вектор-столбцы в системах I и E соответственно, а элементами матрицы τ служат направляющие косинусы осей ξ,η,ς.

Чтобы убедиться в этом, рассмотрим, например, преобразование координат на плоскости (рис. 8.12). Из геометрических соображений следуют уравнения преобразования координат:

X = cosφ ξ – sinφ η,

Y = sinφ ξ– cos φ η

Эти же уравнения в векторах пространства E и I представлены в виде (8.1) в другой форме записи с помощью векторно-матричной символики. Отсюда следует, что элементами матрицы τ служат направляющие косинусы осей ξ,η относительно осей x,y. Это справедливо и для трехмерного пространства.

Записанные выше уравнения известны в математике как уравнения преобразования координат. Они используются очень часто в разнообразных геометрических задачах, где необходимо совершить переход от одной координатной системы к другой.

Рис.8.12. Преобразование координат на плоскости

Аналогичным образом для случая пространственного преобразования координат, имеющего дело с трехмерными векторами можно получить матрицу τ:

,

Эту матрицу τ используют для задания ориентации тела в пространстве.

Пусть с твердым телом, которое для большей наглядности представим в виде параллелепипеда, оси связаны таким образом, что совпадают с ребрами a, b, c (рис. 8.13).

Рис. 8.13 Последовательность трех поворотов твердого тела

вокруг трех осей, связанных с телом

В начальном положении тела оси i_1, i₂, i₃ совпадают с одноименными неподвижными осями e_1, e₂, e₃. Повернем тело вокруг ребра a на угол φ₁ — это первый поворот. В новом положении тела ребра a, b, c определяют новое положение связанной системы — базис I₁. Произведем второй поворот вокруг ребра b на угол φ₂ В новом положении ребра a, b, c определяют базис I₂. Осуществим третий поворот — вокруг ребра с на угол φ₃. Координаты некоторой точки M, принадлежащей твердому телу, для каждой пары систем связаны уравнениями

r_M⁽²⁾ = T₃ r_M;

r_M⁽¹⁾ = T₂ r_M⁽²⁾ ;

R_{M =} T₁ r_M⁽¹⁾,

откуда следует:

R_M=T₁T₂T₃; (8.2)

t=T₁T₂T₃. (8.3)

Последовательные повороты дают последовательные линейные преобразования координат. Их можно представить в виде одного линейного преобразования с матрицей, равной произведению матриц последователь-ных преобразований, причем матрицы расставляются слева направо в порядке следования поворотов.

Из теоретической механики известно что, три последовательных поворота вокруг различных осей задают произвольную ориентацию тела.

Вычислим матрицы операторов преобразования координат, соответствующие поворотам тема вокруг координатных осей. Такие повороты будем называть элементарными. Итак, пусть системы x,y,z и xhz — прямоугольные, одинаково ориентированные системы координат с началом в одной и той же точке О. За положительное направление примем вращение против часовой стрелки, если смотреть с положительного направления оси поворота.

Рис. 8.14. Элементарный поворот вокруг оси x

Предположим, что система xhz получена из системы x,y,z поворотом на угол ψ в положительном направлении вокруг оси ox (рис. 8.14). Соответствующий оператор преобразования координат обозначим X. Для его матрицы имеем

Матрица X составлена из направляющих косинусов осей xhz.

Подобным образом, если системa xhz, получена из x,y,z поворотом в положительном направлении на угол θ вокруг оси oy, для соответствующего оператора преобразования координат Y находим матрицу

Наконец, если система xhz получена из системы координат x,y,z поворотом в положительном направлении на угол φ вокруг оси oz, для матрицы соответствующего оператора преобразования координат Z имеем

8.7. Кинематика манипулятора

Манипулятор представляет физический аналог системы, в которой происходит многократное, последовательное преобразование пространств, связанных со звеньями манипулятора, в неподвижное рабочее пространство. Поэтому исследование его кинематики будет сводиться к разбиению всей системы на пары пространств и к последовательному применению соответствующих этим преобразованиям кинематических соотношений. Рассмотрим вначале эти соотношения.

Вращение твердого тела вокруг неподвижной точки при совмещении начала связанной с телом координатной системы xhz с неподвижной точкой тела задается при помощи оператора преобразования координат (он же оператор поворота)

R = t r. (8.7)

Найдем вектор скорости некоторой точки М этого тела в неподвижном пространстве. Для этого продифференцируем по времени записанное выше соотношение. После дифференцирования и некоторых последующих преобразований получим

V = W R,

где W - кососимметрическая матрица вида

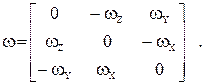
Матрица W сформирована на основе компонентов вектора угловой скорости w = [ w_x, w_y, w_z ].

После дифференцирования уравнения для скорости получим формулу для ускорения точки М:

a=(E + W²) R,

где E – кососимметрическая матрица, составленная из компонентов вектора углового ускорения ε = [ ε_x,ε_y,ε_z ] по той же схеме, что и приведенная выше матрица W.

Рассмотрим общий случай движения твердого тела, который задается векторным равенством

R = R_A + t r, (8.8)

где R_A - радиус-вектор полюса связанной системы осей (рис.8.15).

Дифференцируя это равенство по времени, получим выражение для скорости точки М, принадлежащей твердому телу:

V = V_A + W (R – R_A), (8.9)

где V_A - скорость полюса - точки А. Матрица W характеризует вращательное движение тела.

Рис. 8.15. Общий случай движения твердого тела

Дифференцируя полученную формулу еще раз по времени, получим выражение для ускорения:

a=a_A+E(R-R_A)+W²(R-R_A), (8.10)

где E кососимметричная матрица, составленная также как матрица W, но из компонентов углового ускорения вращательного движения твердого тела.

Заметим, что в записанных выше формулах фигурируют векторы абсолютной скорости и абсолютного ускорения тела, т.е. скорости и ускорения относительно неподвижной системы координат. Для определения этих векторов в случае исследования движения манипуляторов нужно уметь определять их значения по известным параметрам относительного вращательного движения, т.е. по параметрам движения в шарнирах манипулятора.

Рассмотрим операции сложения угловых скоростей и угловых ускорений в векторно- матричной формулировке.

Пусть I - координатное пространство, соответствующее координатной системе, жестко связанной с твердым телом (рис.8.16). Предположим, что задано еще одно подвижное пространство I₁. Наконец Е - неподвижное пространство.

Пусть задано вращение твердого тела относительно пространства I₁, а также движение пространства I₁ относительно неподвижного пространства E. В таком случае, как известно из теоретической механики, угловая скорость абсолютного движения твердого тела равна сумме угловых скоростей первого и второго относительного движения. Векторы относительных скоростей первого и второго движения должны быть приведены к неподвижному пространству:

Не нашли, что искали? Воспользуйтесь поиском: