Метод равных и наименьших относительных отклонений

В этом методе вместо многокритериальной задачи решается несколько однокритериальных задач по каждому из критериев в отдельности следующим образом.

1. Находится оптимальное решение по каждому из критериев по отдельности. Система ограничений для каждого из критериев одна и та же.

2. Находится относительное отклонение для каждого из критериев :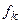

, (1)

где – экстремальное решение задачи по k -му критерию;

– k -й критерий (целевая функция);

K – количество критериев.

3. На основе условия равенства относительных отклонений к системе ограничений задачи добавляется равенство следующего вида (в количестве K – 1):

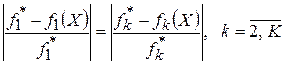. (2)

В каждом последующем добавляемом ограничении слева от знака равенства всегда стоит относительное отклонение для первого критерия, а справа от знака равенства – относительное отклонение для последующего критерия, .

4. Поскольку относительные отклонения должны быть наименьшими, итоговая целевая функция будет иметь вид

. (3)

Т.е., целевая функция представляет собой минимум относительного отклонения для какого-то одного критерия (любого, обычно последнего).

Замечания.

1) Необходимо учитывать, что чтобы минимизировать критерий 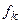, достаточно максимизировать функцию вида – 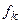, так как .

Таким образом, если оба приравниваемые относительные отклонения определены по максимизируемым критериям, знаки модуля опускаются.

Например, два первых приравниваемых относительных отклонения определены по максимизируемым критериям:

.

Опустив знаки модуля и преобразовав это ограничение, получим ограничение вида

и далее

Если одно из приравниваемых относительных отклонений определено по максимизируемому критерию, а второе – по минимизируемому критерию, то, опустив знаки модуля, перед вторым относительным отклонением необходимо поставить знак минус.

Предположим, что, первое приравниваемое относительное отклонение определено по максимизируемому критерию, а другое приравниваемое относительное отклонение определено по минимизируемому критерию, поэтому перед правой частью равенства поставлен знак минус.

Опустив знаки модуля и преобразовав это ограничение, получим ограничение вида

и далее

2) Решение может быть неэффективным, поэтому предварительно необходимо выделить область компромиссов.

Пример. Решить задачу

методом равных и наименьших отклонений.

Решение

1. Решаем только по первому критерию.

Находим f ₁^*=160.

2. Решаем только по второму критерию.

Находим f ₂^*=1800.

3. Находим относительные отклонения для каждого критерия:

.

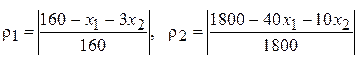
Поскольку оба критерия максимизируются, знак модуля можно опустить. Приравнивая величины отклонений , получаем дополнительное ограничение вида :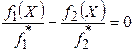

.

Итоговая целевая функция будет иметь вид .

Окончательно задача примет вид:

Врезультате решения Х ^*=(27,3; 32,9); f ₁ (X^*) = 125,8; f2 (X^*) = 1413.

Не нашли, что искали? Воспользуйтесь поиском: