
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Вопрос 20. Транспортная задача линейного программирования
Транспортная задача – это задача разработки наиболее экономичного плана перевозки продукцииодного вида (из нескольких пунктов отправления в пункты назначения), т. е. определения того, сколько груза должно быть отправлено из каждого i -го пункта отправления (от поставщика) в каждый j- й пункт назначения (до потребителя)с минимальными транспортными издержками
Условие транспортной задачи обычно записывается в виде таблицы 7.1, в которой п потребителей однородного груза размещаются по столбцам, а т поставщиков - по строкам. В последнем столбце таблицы проставляют запас аi (i = 1, m) груза, имеющийся у каждого поставщика, а в последней строке - потребность в нем потребителей (спрос) bj (j = 1, п). На пересечении строк со столбцами (в клетках таблицы) записывают затраты сij на перевозку единицы груза по этим маршрутам (величина транспортных расходов задается с помощью тарифов на перевозку единицы продукции). В клетках таблицы также могут указываться размер поставки, или расстояние пробега по всем возможным маршрутам, или время доставки груза.
Размер поставки продукции i- м поставщиком j -му потребителю обозначим хij;общую сумму затрат на перевозку груза обозначим через F.
Таблица 7.1 – Условие транспортной задачи
| Потребители | ||||||||
| Поставщики | П1 | П2 | ... | П j | ... | Пn | Запас | |
| П1 | c 11 | c 12 | ... | c 1 j | ... | c 1 n | а1 | |
| П2 | c 21 | c 22 | ... | c 2 j | ... | c 2 n | а2 | |
| ... | ... | ... | ... | ... | ... | ... | ... | |
| П i | ci 1 | ci 2 | ... | cij | ... | cin | аi | |
| ... | ... | ... | ... | ... | ... | ... | ... | |
| Пm | cm 1 | cm 2 | ... | cmj | ... | cmn | аm | |
| Спрос | b 1 | b 2 | bj | ... | bn |
Транспортная задача, для которой выполняется условие равенства суммы запасов аi груза у поставщиков и суммарного спроса bj потребителей

называется закрытой, а в противном случае открытой.
Запишем математическую модель закрытой транспортной задачи (запас груза у поставщиков равняется суммарному спросу потребителей):
1) объем поставок i -гo поставщика должен равняться количеству имеющегося у него груза:

2) объем поставок j -му потребителю должен быть равен его спросу:

3) запас груза у поставщиков должен равняться суммарному спросу потребителей:

4) размер поставок должен выражаться неотрицательным числом:
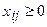
5) общая сумма затрат на перевозку груза должна быть минимальной:
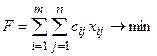
Математические модели закрытой и открытой транспортных задач представлены в таблице 2.
Таблица 2 – Математические модели транспортных задач
| Закрытая транспортная задача | Открытаятранспортная задача | |
Целевая функция 
| ||
запас груза у поставщиков равен суммарному спросу потребителей:

| Запас груза у поставщиков больше суммарного спроса потребителей: 
| Запас груза у поставщиков меньше суммарного спроса потребителей: 
|
| Ограничения на поставщиков: | ||
объем поставок i -гo поставщика равен количеству имеющегося у него груза:

| размер поставок ≤ суммы запасов груза:
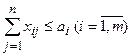
| размер поставок = сумме запасов груза:

|
| Ограничения на потребителей: | ||
объем поставок j -му потребителю равен его спросу:

| размер поставок = суммарному спросу: 
| размер поставок ≤ суммарному спросу:

|
Размер поставки продукции 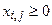
|
Далее рассмотрены наиболее часто встречающиеся дополнительные ограничения и условия, используемые при решении транспортных задач.
1 Запрет перевозок от i -го поставщика j- му потребителю достигается за счет добавления ограничения следующими способами: а) за счет введения в математическую модель задачи дополнительного ограничения, устанавливающего количество перевозимого груза равным нулю  (при решении в среде MS Excel); б) за счет введения стоимости перевозки единицы груза намного большей (на несколько порядков), чем стоимости остальных перевозок (при решении методом потенциалов).
(при решении в среде MS Excel); б) за счет введения стоимости перевозки единицы груза намного большей (на несколько порядков), чем стоимости остальных перевозок (при решении методом потенциалов).
2 Требование фиксированной поставки: если нужно перевезти строго определенное количество d груза, то добавляется ограничение  .
.
3 Наличие нижней или верхней границ поставок. Нижняя граница поставки: если нужно перевезти не менее некоторого количества d груза, то добавляется ограничение  . Верхняя граница поставки: если нужно перевезти не более некоторого количества d груза, то добавляется
. Верхняя граница поставки: если нужно перевезти не более некоторого количества d груза, то добавляется  .
.
4 Максимизация целевой функции в некоторых моделях транспортного типа. Многие экономические задачи (например, оптимальное закрепление за станками операций по обработке деталей, распределение сельскохозяйственных культур за посевными площадями участков земли) также сводятся к решению транспортной задачи. Правда, как правило, в этих случаях необходимо находить максимум функции (количество обработанных деталей, суммарный сбор зерна должны быть как можно большими).
Транспортная задача может быть решена, например, методом потенциалов. Далее будет изучен самый простой способ решения этой задачи – с помощью надстройки Поиск решения в среде MS Excel.
Пример
У двух поставщиков А1, А2 имеется однородный груз в количествах, соответственно равных 10 и 15 ед. Этот груз требуется перевезти трем потребителям В1, В2 и В3 соответственно в количествах 5, 10 и 15 ед. Стоимость доставки единицы груза из каждого пункта отправления в соответствующие пункты назначения задана таблицей 1 тарифов (тыс. руб. за ед. груза). Найти решение транспортной задачи зерна из условия минимизации транспортных расходов при дополнительных условиях: из А1 в В2 – не более 2 ед. груза, из А2 а В3 должно быть перевезено не менее 5 ед. груза, из А2 в В1 груз доставить невозможно.
Таблица 1
| Пункты отправления (поставщики) | Пункты назначения (потребители) | Запасы | ||
| В1 | В2 | В3 | ||
| А1 | ||||
| А2 | ||||
| Спрос (потребности) |
Решение
Данная транспортная задача открытого типа, причем запас груза у поставщиков меньше суммарного спроса потребителей. Суммарный объем запасов составляет 10+15=25 ед., а суммарный спрос – 5+10+15=30 ед., т.е. кто-то из потребителей недополучит требуемый объем груза, что учтено в ограничении на потребителей знаком ≤. Поскольку запас будет использован полностью, это учтено в ограничении на поставщиков знаком =.
Обозначим через xij – количество груза, перевозимое от i -го поставщика j -ому потребителю,  ,
,  .
.
Математическая модель задачи имеет вид:
Ограничения:

Целевая функция:

Оформим решение задачи на листе Excel (рисунок 1).
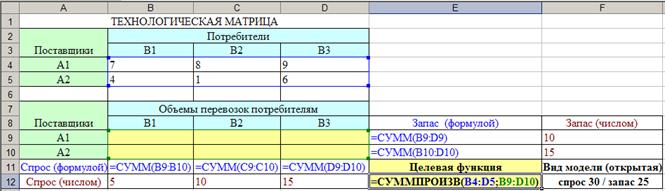

Рисунок 1
В параметрах решения задачи необходимо указать «Линейная модель» и «Неотрицательные значения».
После нажатия кнопки Выполнить получаем ответ, представленный на рисунке 2.
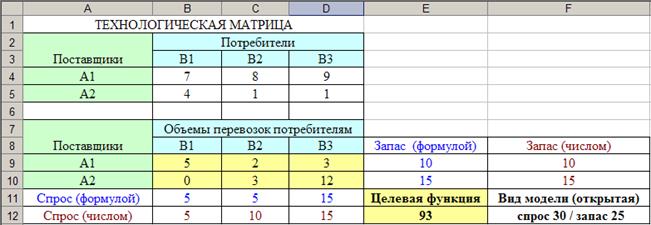
Рисунок 2
Оптимальный план перевозки продукции с минимальными расходами по ее доставке следующий:
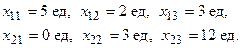
Таким образом, из пункта А1 в В1 перевозится 5 ед. груза, в В2 – 2 ед., в В3 – 3 ед.; из А2 в В1 – 0 ед. груза, в В2 – 3 ед., в В3 – 12 ед. Общие минимальные трансп. расходы составят 93 тыс. руб.
Не нашли, что искали? Воспользуйтесь поиском: