Вопрос 17. Формы записи задачи линейного программирования, их эквивалентность и способы преобразования

Модель задачи линейного программирования (ЗЛП) может быть записана в одной из приведенных ниже форм:

1 Общая, или произвольная, форма записи:

при ограничениях:

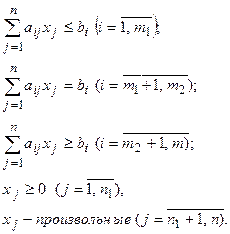
где c_j, a_ij, b_i — заданные действительные числа.

2 Симметричная, или стандартная, форма записи:

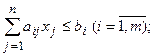
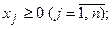
3 Каноническая, или основная, форма записи:

.

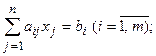
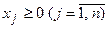Указанные выше три формы записи ЗЛП эквивалентны в том смысле, что каждая из них с помощью несложных преобразований может быть сведена к другой форме.

При необходимости задачу минимизации можно заменить задачей максимизации, и наоборот. Очевидно, что минимальное значение функции F (x) равно максимальному значению функции – F (x), взятому с противоположным знаком, т.е.

min F (x) = – max(– F (x)).

Неравенство типа > путем умножения левых и правых частей на –1 можно превратить в неравенство типа <, и наоборот.

Ограничения-неравенства

преобразуются в ограничения-равенства путем прибавления (вычитания) к левым частям дополнительных (балансовых) неотрицательных переменных x _{n + i} > 0:

.

В случае необходимости ограничение-равенство

можно записать в виде системы неравенств

Если в ЗЛП какая-то переменная x_k не подчинена условию неотрицательности, ее заменяют разностью двух других неотрицательных переменных х'_k > 0 и х"_k > 0:

x_k= х'_k - х"_k.

Не нашли, что искали? Воспользуйтесь поиском: