Вопрос 12. Автокорреляция уровней временного ряда

При наличии трендовой и сезонной составляющих значения каждого последующего уровня ряда зависят от предыдущих значений. Корреляционную зависимость между последовательными уровнями временного ряда называют автокорреляцией уровней ряда.

Ее можно измерить с помощью коэффициента автокорреляции уровней ряда, т.е. между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во времени. Число периодов, по которым рассчитывают коэффициент автокорреляции, называется лагом.

С увеличением лага число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается.

Коэффициент автокорреляции уровней ряда первого порядка (он измеряет зависимость между соседними уровнями ряда t и t –1, т.е., при лаге, равном единице.

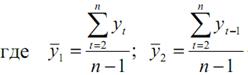
Переменные у – это составляющие временного ряда.

Коэффициент автокорреляции уровней ряда второго порядка

Коэффициенты автокорреляции более высоких порядков определяют аналогично.

Последовательность коэффициентов автокорреляции уровней первого, второго и т.д. порядков называют автокорреляционной функцией временного ряда, а график зависимости ее значений от величины лага (число периодов, по которым рассчитывается коэффициент автокорреляции) — коррелограммой.

При помощи анализа автокорреляционной функции и коррелограммы можно выявить структуру ряда.

Если наиболее высоким оказался коэффициент автокорреляции первого порядка, исследуемый временной ряд содержит только трендовую составляющую.

Если наиболее высоким оказался коэффициент автокорреляции порядка t, ряд содержит сезонные циклические колебания с периодичностью t моментов времени.

Если ни один из коэффициентов автокорреляции не оказался значимым, можно сделать предположение относительно структуры этого ряда:

– либо ряд не содержит трендовую и сезонную составляющие и имеет структуру, сходную со структурой ряда на рисунке 1, в (где изображена случайная (Е) компонента),

– либо ряд содержит сильную нелинейную тенденцию, для выявления которой нужно провести дополнительный анализ.

Не нашли, что искали? Воспользуйтесь поиском: