
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Вопрос 16. линейные экономико-математические модели
Рассмотрим пример. Фирма производит и продает столы и шкафы из древесины хвойных и лиственных пород. Расход каждого вида в кубометрах на каждое изделие задан в таблице.
| Расход древесины, м3 | Цена изделия, тыс. руб. | ||
| хвойные | лиственные | ||
| Стол | 0,15 | 0,25 | 0,7 |
| Шкаф | 0,3 | 0,1 | 1,3 |
| Запасы древесины |
Определить оптимальное количество столов и шкафов, которое следует поставлять на продажу для получения максимального дохода фирмы.
Решение. Прежде чем построить математическую модель задачи, т.е. записать ее с помощью математических символов, необходимо четко разобраться с экономической ситуацией, описанной в условии. Для этого необходимо с точки зрения экономики, а не математики, ответить на следующие вопросы:
1) Какова цель решения? Какой параметр задачи служит критерием оптимальности решения, например, прибыль, себестоимость, время и т.д. В каком направлении должно изменяться значение этого параметра (к max или к min) для достижения наилучших результатов? Т.е. каков вид экстремума целевой функции – max или min?
2) Что является входными параметрами, т.е. искомыми величинами задачи?
3) Какие ограничения в отношении искомых величин и ресурсов задачи должны быть выполнены?
Только после экономического ответа на все эти вопросы можно приступать к записи этих ответов в математическом виде, т.е. к записи математической модели.
Цель решения – максимальный доход. Критерий оптимальности – доход. Вид экстремума целевой функции – максимум. Максимальный доход складывается из суммы произведений цен изделий и количеств изделий. Цены известны из исходных данных. Искомыми величинами являются количества выпускаемых изделий, которые обозначим следующим образом: через х 1 – количество столов, х 2 – количество шкафов.
Целевая функция имеет вид f = 0,7 ∙ х 1 + 1,3 ∙ х 2 ® max
Система ограничений включает ограничения трех видов:
1) ограничения на запасы древесины
0,15∙ х 1 + 0,3∙ х 2 £ 100
0,25∙ х 1 + 0,1∙ х 2 £ 50
2) условие неотрицательности переменных
х 1, х 2 ≥ 0
3) условие целочисленности переменных.
Для решения задач оптимизации в Excel существует инструмент «Поиск решения», доступ к которому осуществляется из надстройки «Пакет анализа».
Решение задачи в Excel:
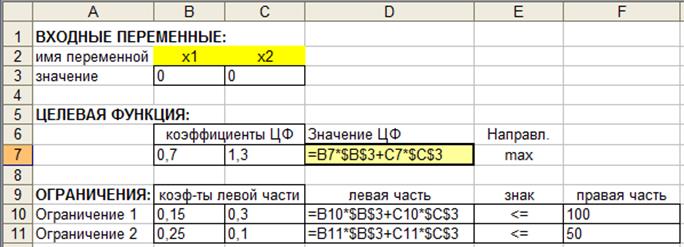
В ячейки В3:С3 будет помещен результат, в ячейках В7:С7 записаны коэффициенты целевой функции, в ячейки В10:С11 занесены ограничения, в ячейки F10:F11 занесены имеющиеся запасы.
В диалоговом окне Поиск решения в поле Установить целевую ячейку вводим ячейку D7, устанавливаем переключатель Равной в положение «максимальному значению», в поле Изменяя ячейки вводим диапазон ячеек В3:С3, в поле Ограничения вводим ограничения:
D10 <= F10
D11 <= F11
В3:С3 >= 0
В3:С3 = цел (рисунок 3).
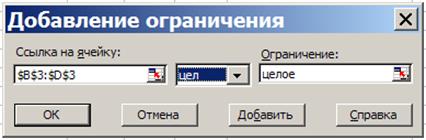
Рис.3 – Ввод условия целочисленности переменных задачи
После нажатия кнопки Выполнить получаем ответ, представленный на рисунке.

Ответ: следует выпускать 84 стула и 290 шкафов.
Не нашли, что искали? Воспользуйтесь поиском: