Вопрос 13. Выбор вида уравнения тренда

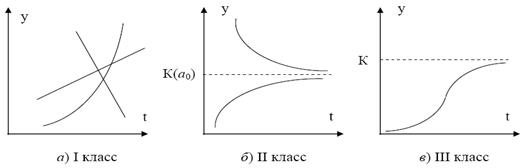
I класс) Процессы с монотонным характером развития и отсутствием пределов роста (рис а). Эти условия справедливы, например, для большинства натуральных показателей промышленного производства. Для моделирования такого тренда могут использоваться линейная 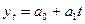, степенная , экспоненциальная функции .

Полином первой степени на графике изображается прямой и используется для описания процессов, развивающихся во времени равномерно. Полином второй степени применим в тех случаях, когда процесс развивается равноускоренно (т.е. имеется равноускоренный рост или равноускоренное снижение уровней). Использовать для опреде­ления тренда полиномы выше третьего высоких степеней нецелесообразно, поскольку полученные таким образом аппроксимирующие функции будут отражать случайные отклонения (что противоречит смыслу тенденции).

I I класс) Процессы с «насыщением», которые имеют предел роста (падения) в исследуемом периоде. Развитие процесса происходит под влиянием некоторых ограничивающих факторов, величина воз­действия которых растет вместе с ростом достигнутого уровня. С такими про­цессами часто сталкиваются в демографии, при изучении потребностей в товарах и услугах (в расчете на душу населения), при исследовании эффективности ис­пользования ресурсов и т. д. Примерами показателей, для которых могут быть указаны пределы роста, являются среднедушевое потребление определенных продуктов питания, расход удобрений на единицу площади и т. п.

В этом случае для моделирования тенденции используются гиперболическая функция

либо модифицированная экспонента

с параметром а ₁, удовлетворяющим условию 0 <а₁ < 1.

В этих двух функциях параметры а ₀ и К равны пределу роста

III класс. Так называемые S-образные процессы (рис. 2. в), представляющие как бы два последовательных лавинообразных процесса (когда прирост зависит от уже достигнутого уровня): один с ускорением развития, а другой - с замед­лением. С такими процессами часто сталкиваются в демографических иссле­дованиях, в страховых расчетах, при решении задач прогнозирования научно-технического прогресса, при определении спроса на новый вид продукции.

К S-образным процессам можно отнести процесс развитие новой отрасли (нового производства). Вначале производство развивается очень медленно вследствие того, что технические методы производства еще недостаточно раз­работаны, издержки производства высоки и спрос на рынке на данный товар еще очень мал. поэтому производство развивается медленно. В дальнейшем. благодаря усовершенствованию технических методов изготовления, переходу к массовому производству и увеличению емкости рынка для данного товара про­изводство растет быстрее. Затем наступает период насыщения рынка, рост про­изводства все более замедляется, и. наконец, почти прекращается. Наступает стабилизация производства на определенном уровне. Следует отметить, что выявленные закономерности развития следует обобщать с определенной осто­рожностью и. причем, только для достаточно коротких периодов, так как выяв­ленная тенденция развития производства может быть нарушена вследствие внешних факторов, например, технического переворота в данной отрасли или связанных с нею.

Для моделирования тренда S-образных процессов используют либо логистическую функцию 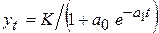с параметром а ₁<1, либо кривую Гомперца 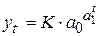с параметрами, удовлетворяющими условиям 0 < а ₀, а ₁<1. Предел роста в обоих случаях равен параметру К.

Выбор наилучшего уравнения тренда можно осуществить путем перебора основных видов тренда (линейного, экспоненциального, степенного и т.д.), расчета по каждому уравнению коэффициента детерминации R ² и выбора уравнения тренда с максимальным значением R ². Оценки параметров уравнений тренда находят методом наименьших квадратов.

Содержание экономико-математических моделей и методика их построения

Вопрос 14. Содержание экономико-математических моделей и методика их построения

Содержанием любой экономико-математической модели является выраженная в формально-математических соотношениях экономическая сущность условий задачи и поставленной цели.

Чтобы сформулировать и решить конкретную экономическую задачу, необходимо выполнить следующие действия:

1 Определить цели. Цель – желаемое состояние экономической системы для одного из участников экономической системы.

2 Определить критерий оптимальности – экономический показатель, выражающийся при помощи целевой функции через другие экономические показатели, и отражающий степень достижения цели. По значению критерия выбирается оптимальный вариант из всех возможных.

3 Выбрать входные параметры. Входным параметром x_i называется неизвестная переменная величина, изменение которой приводит к изменению критерия оптимальности.

4 Определить целевую функцию. Целевая функция представляет собой уравнение, связывающее значение критерия оптимальности и значения входных параметров

F = f (x ₁, x ₂ ... x_n) → extr. Экстремум – это max (min). Целевая функция позволяет выбрать наилучший вариант из множества возможных, который доставляет экстремум целевой функции.

5 Определить ограничения модели. Они должны отражать все основные условия. Однако практически учесть все условия для достижения цели невозможно, достаточно учесть основные условия. Естественно, полученная модель будет упрощенной по сравнению с реальной.

Математическая модель экономической системы – это целевая функция с набором ограничений.

Допустимое решение – это совокупность чисел 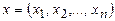, удовлетворяющих ограничениям задачи. Модель имеет множество допустимых решений.

Оптимальное решение математической модели – это значения входных параметров x₁, x₂... x_n, доставляющие экстремум целевой функции F.

Математически общую модель задачи можно представить в виде:

Найти значения n переменных x₁,x₂,…,x_n, которые удовлетворяют системе ограничений

где b_i – некоторое число

и максимизируют или минимизируют целевую функцию

.

Если на переменные налагается условие неотрицательности, тогда в модель задачи вводится условие .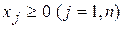

Иногда еще на переменные налагается условие целочисленности.

Формулировка каждой задачи оптимизации должна требовать экстремального значения лишь одной величины, т.е. одновременно системе не должно приписываться два и более критериев оптимизации, т.к. практически всегда экстремум одного критерия не соответствует экстремуму другого. Приведем примеры.

Типичный пример неправильной постановки задачи оптимизации:

«Получить максимальную производительность при минимальной себестоимости».

Ошибка заключается в том, что ставится задача поиска оптимальности 2-х величин, противоречащих друг другу по своей сути.

Правильная постановка задачи могла быть следующая:

а) получить максимальную производительность при заданной себестоимости;

б) получить минимальную себестоимость при заданной производительности;

В первом случае критерий оптимизации - производительность а во втором - себестоимость.

Не нашли, что искали? Воспользуйтесь поиском: