
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Методы устранения мультиколлинеарности.
Единого метода устранения мультиколлинеарности, годного в любом случае, нет, т.к. причины и последствия мультиколлинеарности неоднозначны и во многом зависят от рез-тов выборки.
Методы:
1) исключение из модели одной или ряда коррелированных переменных;
2) получение дополнительных данных или новой выборки;
3) изменение спецификации модели: либо изменяется форма модели, либо добавляются объясняющие переменные, не учтенные в первоначальной модели, но существенно влияющие на зависимую переменную.
Рассмотрим более подробно первый метод. Отсев факторов можно проводить, например, по t -критерию Стьюдента для коэффициентов регрессии: из уравнения исключаются факторы с величиной t -критерия меньше табличного.
Наиболее широко в процедуре отсева используется матрица парных коэффициентов корреляции
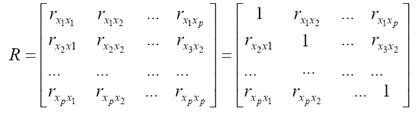
Коэффициенты парной корреляции  между объясняющими переменными используются для выявления дублирующих факторов. Линейная зависимость между объясняющими переменными xi и xj считается установленной, если выполняется условие
между объясняющими переменными используются для выявления дублирующих факторов. Линейная зависимость между объясняющими переменными xi и xj считается установленной, если выполняется условие  > 0,8, а сами факторы называются явно коллинеарными (эмпирическое правило). Один из факторов должен быть исключен из модели. Предпочтение при этом отдается тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами.
> 0,8, а сами факторы называются явно коллинеарными (эмпирическое правило). Один из факторов должен быть исключен из модели. Предпочтение при этом отдается тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами.
Наряду с парной коллинеарностью может иметь место линейная зависимость между более, чем двумя переменными. Для оценки мультиколлинеарности факторов в этом случае может использоваться величину определителя 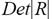 матрицы парных коэффициентов корреляции
матрицы парных коэффициентов корреляции 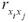 между факторами либо ее минимального собственного значения.
между факторами либо ее минимального собственного значения.
Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность между факторами и тем ненадежнее результаты множественной регрессии.
При исключении из регрессии факторов предпочтение отдается не фактору, более тесно связанному с результатом у, а тому фактору, который при достаточно тесной связи с результатом у имеет наименьшую тесноту связи с другими факторами.
Пример. При изучении зависимости y = f (x, z, u) матрица парных коэффициентов корреляции оказалась следующей:
| y | x | z | р | |
| y | ||||
| x | 0,8 | |||
| z | 0,7 | 0,8 | ||
| р | 0,6 | 0,5 | 0,2 |
Очевидно, что факторы x и z дублируют друг друга. В уравнение целесообразно включить фактор z, а не х, так как корреляция z с результатом у слабее, чем корреляция фактора x с у (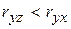 ) и имеется еще более слабая межфакторная корреляция
) и имеется еще более слабая межфакторная корреляция 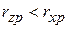 . Поэтому в данном случае в уравнение множественной регрессии включаются факторы z и р.
. Поэтому в данном случае в уравнение множественной регрессии включаются факторы z и р.
Не нашли, что искали? Воспользуйтесь поиском: