Модели множественной линейной регрессии.

Множественной регрессией называют уравнение связи с несколькими независимыми переменными:

. (2.1)

Множественная регрессия применяется, когда из множества факторов, влияющих на результативный признак, нельзя выделить один доминирующий фактор и необходимо учитывать влияние нескольких факторов.

Построение уравнения множественной регрессии осуществляется в два этапа [3, с. 13]:

1) спецификация модели;

2) оценка параметров выбранной модели.

В свою очередь, спецификация модели включает выполнение двух этапов:

– отбор р факторов , подлежащих включению в модель;

– выбор вида аналитической зависимости .

Для оценки параметров уравнения множественной регрессии обычно при­меняется метод наименьших квадратов.

Основная цель множественной регрессии - построить модель с нескольки­ми факторами и определить при этом влияние каждого фактора в отдельности, а также их совместное воздействие на изучаемый показатель.

Наиболее часто используются линейная и степенная зависимости.

Для оценки параметров уравнения множественной регрессии обычно при­меняется метод наименьших квадратов.

Для оценки качества полученного уравнения множественной регрессии (2.1) можно использовать коэффициент детерминации 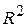. Низкое значение (близкое к 0) коэффициента (индекса) детерминации означает, что в регрессионную модель не включены существенные факторы, с одной стороны, а с другой – рассматриваемая форма связи не отражает реальные соотношения между переменными, включенными в модель. Чем выше значения 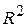, тем лучше данная модель согласуется с данными наблюдений.

Значимость уравнения множественной регрессии в целом так же, как и в парной регрессии, оценивается с помощью F -критерия Фишера.

Оценка значимости коэффициентов регрессии осуществляется с помощью t -критерия Стьюдента.

Не нашли, что искали? Воспользуйтесь поиском: