Предмет и область применения эконометрики.

Слово «эконометрика» представляет собой комбинацию двух слов: «экономика» и «метрика» (от греч. «метрон»). Термин эконометрика введен в научную литературу в 1930 году норвежским статистиком Рагнаром Фришем. Зарождение эконометрики является следствием междисциплинарного подхода к изучению экономики. Эконометрика как наука возникла в первой половине 20-го века в результате активного использования для решения задач экономической теории математических и статистических методов.

Эконометрика – наука, изучающая количественные закономерности и взаимозависимости в экономике методами математической статистики.

Место эконометрики среди иных наук можно представить в виде следующей схемы:

Задача эконометрики – количественная оценка имеющихся взаимосвязей между экономическими явлениями и процессами.

В основе любого эконометрического исследования лежит построение экономико-математической модели, адекватной изучаемым реальным экономическим явлениям и процессам.

Процесс построения эконометрических моделей начинается с качественного исследования проблемы методами экономической теории, формулируются цели исследования, выделяются факторы, влияющие на изучаемый показатель, и формулируются предположения о характере предполагаемой зависимости. На этой основе изучаемые зависимости выражаются в виде математических формул и соотношений

Базой для эконометрических исследований служат данные официальной статистики, либо данные бухгалтерского учета.

Эконометрическое моделирование реальных социально-экономических процессов и систем обычно преследует два типа целей: 1) прогноз экономических и социально-экономических показателей, характеризующих состояние и развитие анализируемой системы; 2) имитацию различных возможных сценариев социально-экономического развития анализируемой системы (многовариантные сценарные расчеты, ситуационное моделирование).

Парная регрессия

Парная (простая) регрессия – уравнение связи двух переменных y и x: y = f (x),

где y – зависимая переменная (результативный признак), функция отклика, эндогенная (внутренняя) пере­менная. Термин «внутренний» отражает тот факт, что значения зависимой переменной у опре­деляются только значениями независимых переменных x.

х – независимая, объясняющая переменная, фактор, входная переменная, внешняя или экзогенная переменная. Термин «внешний» говорит о том, что значения пе­ременных х определяются вне рассматриваемой модели, для которой они яв­ляются заданными.

Уравнения связи функции отклика и факторов называют уравнением регрессии, функцию f – функцией регрессии, а ее график – линией регрессии. В случае единственной входной переменной регрессию называют парной (простой), в общем случае – если входных переменных две и более – множественной.

Парная регрессия применяется, если имеется доминирующий фактор, ко­торый и используется в качестве объясняющей переменной.

Различают линейные и нелинейные регрессии.

Линейная парная регрессия является одной из наиболее распространенных эконометрических моделей и описывается уравнением:

y = b₀ + b₁ · x + ε

где ε – случайная составляющая, учитывающая влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения.

Нелинейные регрессии делятся на два класса:

––– нелинейные по объясняющим переменным, но ли­нейные по оцениваемым параметрам:

полиномы разных степеней

––– нелинейные по оцениваемым параметрам:

степенная

показательная и так далее.

Знак «ˆ» («ридж») означает, что между переменными х и у нет строгой функциональной зависимости, поэтому практически в каждом отдельном случае величина у складывается из двух слагаемых:

,

где у – фактическое (экспериментальное) значение результативного признака;

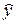– теоретическое значение результативного признака, найденное из уравнения регрессии;

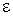– случайная величина, характеризующая отклонения фактического значения у от .

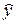Случайная величина e _i включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения [5, с. 44].

Не нашли, что искали? Воспользуйтесь поиском: