Построение уравнения линейной регрессии.

Постановка задачи: По имеющимся данным п наблюдений за совместным изменением двух параметров х и у необходимо определить аналитическую регрессионную зависимость , наилучшим образом описывающую данные наблюдений.

При изучении и построении регрессии выполняют следующие этапы:

1) спецификация уравнения регрессии и определение параметров регрессии;

2) определение степени стохастической взаимосвязи результативного признака и факторов, проверка общего качества уравнения регрессии;

3) проверка статистической значимости каждого коэффициента уравнения регрессии и определение их доверительных интервалов.

Спецификация уравнения регрессии – это выбор вида аналитической зависимости 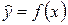. В случае парной регрессии спецификация осуществляется по графическому изображению реальных статистических данных в виде точек в декартовой системе координат, которое называется корреляционным полем (диаграммой рассеивания).

От правильно выбранной спецификации модели зависит величина случайных ошибок: они тем меньше, чем в большей мере теоретические значения результативного признака 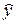подходят к фактическим данным y.

Парная регрессия применяется, если имеется доминирующий фактор, который и используется в качестве объясняющей переменной х.

Простейшей является линейная взаимосвязь между x и y, описываемая линейной функцией регрессии вида .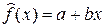

Для вычисления коэффициентов a, b используется метод наименьших квадратов (МНК), который позво­ляет получить такие оценки параметров а и b, при которых сумма квадратов отклонений фактических значений зависимой переменной у от теоретических 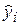минимальна, т. е.

Это означает, что линейная регрессия на диаграмме рассеивания будет проходить «достаточно близко» к точкам (x_i, y_i).

Для линейных уравнений, решается следующая система относительно b ₀и b ₁:

В случае линейной регрессии оценкипараметров b ₀и b ₁находятся следующим образом

Для оценки качества подбора линейной регрессии рассчитывается квадрат линейного коэффициента корреляции, называемый коэффициентом детерминации , а для нелинейной регрессии – квадрат индекса корреляции, называемый индексом детерминации .

Коэффициент детерминации характеризует долю дисперсии 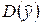результативного признака y, объясняемую регрессией, в общей дисперсии результативного признака. Чем больше доля объясненной вариации, тем меньше роль прочих факторов и тем лучше уравнение регрессии описывает исходные данные. Чем ближе R ² к 1, тем лучше модель описывает (аппроксимирует) исходные данные, и, значит, ее можно использовать для оценки качества построенной модели.

Средняя ошибка аппроксимации – среднее отклонение расчётных значений от фактических. Построенное уравнение регрессии считается хорошего качества, если значение не превышает 8–10 % [5, с. 107].

Не нашли, что искали? Воспользуйтесь поиском: