Оценка значимости уравнения регрессии и его коэффициентов

После того, как найдено уравнение линейной регрессии, про­водится:

1) оценка значимости уравнения в целом с помощью F -критерия Фишера,

2) оценка значимости коэффициентов регрессии с помощью t -критерия Стьюдента.

1) Согласно F -критерию Фишера, выдвигается «нулевая» гипотеза Н₀ о ста­тистической незначимости уравнения регрессии (т. е. о статистически незначи­мом отличии величины F от нуля).

Согласно F -критерию Фишера, выдвигается «нулевая» гипотеза Н ₀остатистической незначимости уравнения регрессии (т. е. о статистически незначимом отличии величины F от нуля). Если расчетное значение F -критерия 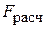превышает табличное 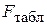, т. е. ,то гипотеза Н ₀отклоняется и принимается статистическая значимость и надежность уравнения регрессии. Если 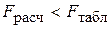, то гипотеза Н ₀не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.

Расчетное значение F -критерия :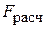

,

где n – число наблюдений;

m – число параметров при переменных х;

R ² – коэффициент детерминации.

Табличное значение F -критерия 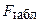определяется по таблицам F -критерия Фишера при числе степеней свободы 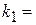m (m – число параметров при переменных х), (n – число наблюдений) и заданному уровню зна­чимости α.

Уровнем значимостиα в статистических гипотезах называ­ется вероятность отвергнуть верную гипотезу. Уровень значимости α обычно принимает значения 0,05 и 0,01, что соответствует вероятности отвергнуть верную гипотезу 5 и 1 %.

2) Возможна ситуация, когда часть вычисленных коэффициентов регрессии не обладает необходимой степенью значимости, т. е. значения этих коэффициентов будут меньше их стандартной ошибки. В этом случае такие коэффициенты должны быть исключены из уравнения регрессии. Поэтому проверка адекватности построенного уравнения регрессии, наряду с проверкой значимости коэффициента детерминации R ², включает в себя также и проверку значимости каждого коэффициента регрессии.

Для оценки статистической значимости коэффициентов регрессии применяется t -критерий Стьюдента, согласно которому выдвигается «нулевая» гипотеза Н ₀о статистической незначимости коэффициента уравнения регрессии (т. е. о статистически незначимом отличии a и b от нуля). Эта гипотеза отвергается при выполнении условия 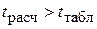, при этом принимается статистическая значимость и надежность проверяемого коэффициента регрессии, т. е. считается, что отличие рассматриваемого коэффициента уравнения регрессии от нуля статистически значимо. Табличное значение t -критерия 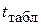определяется по таблице t -критерия Стьюдента по числу степеней свободы 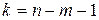и заданному уровню значимости α. Расчетные значения -критерия для каждого коэффициента регрессии ( -статистики Стьюдента) представляют собой отношение оценки коэффициента регрессии к его стандартной ошибке.

t-статистики Стьюдента для коэффициентов регрессии и :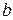

,

Стандартные ошибки коэффициентов линейной регрессии позволяют получить представление о точности полученных оценок коэффициентов регрессии и 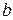, о том, на­сколько далеко они могут отклониться от истинных значений коэффициентов.

, ,

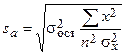где – остаточная дисперсия признака у:

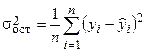
Общая дисперсия 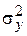результативного признака у отображает влияние как основных, так и остаточных факторов. Остаточная дисперсия результативного признака у отображает влияние только остаточных факторов.

Рассчитанные значения оценок коэффициентов регрессии являются приближенными, полученными на основе имеющихся выборочных данных. Для оценки того, насколько точные значения оценок коэффициентов могут отличаться от рассчитанных, осуществляется построение доверительных интервалов. Доверительные интервалы определяют пределы, в которых лежит точное значение определяемого показателя с заданной вероятностью 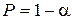[1, с. 131].

Доверительные интервалы для оценок коэффициентов линейной регрессии рассчитываются по формулам:

, ,

где 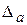, 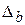– предельные ошибки, рассчитываемые по формулам

, .

Не нашли, что искали? Воспользуйтесь поиском: