Тақырыбы: 4. Электродинамиканың эксперименттік негіздері

Дәріс мақсаты: Электродинамиканың эксперименттік негіздері туралы мағлұмат беру.

1. Кулон заңы және вакуумдағы электростатиканың теңдеулері.

2. Био-Савар-Лаплас заңы және вакуумдағы стационарлық өрістің теңдеулері.

3. Электрмагниттік индукция және Фарадей заңы.

Егер нүктелік зарядтың электростатикалық өрісінде 1-ші нүктеден 2-шіге күштік сызықтың бойымен басқа нүктелік заряд орын ауыстырса, зарядқа әсер етуші күш жұмыс атқарады.

элементар орын ауыстыруындағы күшінің атқаратын жұмысы

.

Сонда зарядты 1-ші нүктеден 2-шіге орын ауыстырғандағы атқарылатын

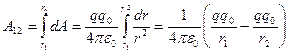(7.6)

өріс күштерінің жұмысы жолдың траекториясына тәуелсіз болады да, бастапқы 1 және соңғы 2 нүктелердің орындарымен ғана анықталады. Бұл қорытынды кез келген электростатикалық өріс үшін орындалады. Демек, электростатикалық өріс потенциалды өріс болып табылады. Күштің потенциалдық өрісінде орналасқан дене потенциалдық энергияға ие болады да, соның есебінен өріс күштері жұмыс атқарады.

Өріс күштерінің атқаратын жұмысы потенциалдық энергияның кемуіне тең:

.

Демек, зарядының электр өрісінде орналасқан зарядының иеленетін потенциалдық энергиясы:

.

Константаның мәні зарядты шексіздікке алыстатқанда (яғни, ), оның потенциалдық энергиясы нөлге тең болатындай етіп таңдап алынады. Бұл жағдайда

Өрістің берілген нүктесіндегі өріс потенциалы деп аталатын

(7.7)

скалярлық шама, кернеулік векторымен қоса, электр өрісін сипаттау үшін пайдаланылады. Сонда зарядты 1-ші нүктеден 2-шіге орын ауыстырғандағы электростатикалық өріс күштерінің атқаратын жұмысын мына түрде жазуға болады

.

Электростатикалық өрістің 1 және 2 нүктелерінің потенциалдар айырмасы бірлік оң зарядты 1-ші нүктеден 2-шіге орын ауыстырғандағы өріс күштерінің атқаратын жұмысына тең:

. (7.8)

Потенциалдың өлшем бірлігі – вольт (В): 1Кл зарядтың 1Дж потенциалдық энергияны иеленетін өріс нүктесінің потенциалы 1В-қа тең деп алынады.

Зарядтар жүйесінің өріс потенциалы әр жеке зарядтың туғызатын өріс потенциалдарының алгебралық қосындысына тең:

(7.9) Электростатикалық өрісте электр зарядын кез-келген тұйық контур бойымен орын ауыстырғандағы атқарылатын жұмыс нөлге тең: .

Егер сыншы заряд Кл тең болса, онда

. (7.10)

Электростатикалық өрістің кернеулік векторының кез келген тұйық контур бойымен алынған циркуляциясы нөлге тең.

Электростатикалық өріс кернеулігі мен потенциал арасындағы байланыс мына теңдеумен өрнектеледі:

немесе . (7.11)

Барлық нүктелеріндегі потенциалдың мәндері бірдей беттерді эквипотенциалды беттер деп атайды.

Кернеулік сызықтар эквипотенциалды беттерге үнемі нормаль бағытталады.

Өріс кернеулігі мен потенциалдың арасындағы байланысты белгілі өріс кернеулігі арқылы өрістің кез келген екі нүктесінің потенциалдар айырмасын анықтау үшін пайдалануға болады.

Кернулігі біртекті электр өрісінде орналасқан жазық бет арқылы өтетін кернеулік векторының ағыны деп

(7.12)

скалярлық шаманы атайды. Мұндағы - кернеулік векторымен бетке жүргізілген нормаль арасындағы бұрыш, - векторының нормальға түсірілген проекциясы.

Біртекті емес өрісте орналасқан кез-келген аудан арқылы өтетін кернеулік векторының ағыны мынаған тең

(2)

Макроскопиялық зарядтарды қарастырғанда олардың дискретті (үздікті) құрылымына көңіл аудармайды да, оларды кеңістіктің әр нүктесінде шектелген тығыздықпен үздіксіз түрде таралады деп есептейді.

Зарядтың сызықтық тығыздығы деп дененің бірлік ұзындығына келетін зарядты атайды: , Кл/м.

Зарядтың беттік тығыздығы деп аудан бірлігіне келетін зарядты атайды: , Кл/м². (16.4)

Зарядтың көлемдік тығыздығы деп дененің бірлік көлеміне келетін зарядты атайды: , Кл/м³

Вакуумдегі электростатикалық өріс үшін Гаусс теоремасы: кез келген тұйық бет арқылы өтетін вакуумдегі электростатикалық өрістің кернеулік векторының ағыны сол бетпен қоршалған зарядтардың алгебралық қосындысының -ге қатынасына тең:

.

1. Екі әр аттас зарядталған өзара параллель шексіз жазықтықтың (жазық конденсатор) арасындағы потенциалдар айырмасы:

, мұндағы - жазықтықтардың ара қашықтығы.

2. Екі зарядталған коаксиалды цилиндрдің (цилиндрлік конденсатор) арасындағы потенциалдар айырмасы: , мұндағы және – цилиндлердің радиустары.

3. Екі зарядталған концентрлі сфераның арасындағы (сфералық конденсатор) потенциалдар айырмасы:

3

Өткізгіштің ішкі бөліктерінде зарядтың болмауы Гаусс теоремасының салдары болып табылады. Ал Гаусс теоремасының өзі Кулон заңына негізделген.

Негізгі сұрақтар:

1. Өріс патенциалы деген не?

2. Кернеулік векторының ағыны неге тең?

3. Эквипотенциал беттер деген не?

4. Вакуумдегі электростатикалық өріс үшін Гаусс теоремасы қалай айтылады?

Не нашли, что искали? Воспользуйтесь поиском: