Программа курса «Математический анализ» Первый семестр 1 страница

РАЗДЕЛ 1. Введение в математический анализ

1. Множества и операции над ними. Примеры числовых множеств. Понятие модуля и окрестности точки.

2. Функция. Способы задания функции. Основные свойства функций. Понятие явной, неявной, обратной и сложной функции. Основные элементарные функции. Понятие элементарной функции.

3. Числовая последовательность. Предел числовой последовательности. Предел функции в бесконечности и в точке.

4. Бесконечно малые величины. Теорема о связи бесконечно малых величин с пределами функций. Свойства бесконечно малых величин. Бесконечно большие величины. Теорема о связи бесконечно больших величин с бесконечно малыми. Свойства бесконечно больших величин.

5. Основные теоремы о пределах. Признаки существования предела. Замечательные пределы.

6. Непрерывность функции в точке. Точки разрыва. Свойства функций, непрерывных в точке. Свойства функций, непрерывных на отрезке.

РАЗДЕЛ 2. Дифференциальное исчисление функции одной переменной

7. Задачи, приводящие к понятию производной. Определение производной. Геометрический и механический смысл производной.

8. Дифференцируемость функции. Теорема о зависимости между непрерывностью функции и дифференцируемостью.

9. Схема вычисления производной. Правила дифференцирования. Теоремы о нахождении производной сложной и обратной функций.

10. Производные основных элементарных функций.

11. Нахождение производных обратных тригонометрических функций. Производная неявной функции. Нахождение производных высших порядков.

12. Основные теоремы дифференциального исчисления (теоремы Ферма, Ролля, Лагранжа). Правило Лопиталя.

13. Возрастание и убывание функции на отрезке. Достаточные условия возрастания и убывания функции.

14. Экстремум функции. Необходимое условие экстремума. Критические точки. Достаточные условия существования экстремума.

15. Нахождение наибольшего и наименьшего значения функции на отрезке.

16. Понятие выпуклости вверх (вниз) функции. Достаточное условие выпуклости вверх (вниз) функции на отрезке.

17. Точка перегиба. Необходимое и достаточное условия перегиба.

18. Определения асимптот графика функции. Теоремы о нахождении вертикальной, горизонтальной и наклонной асимптот.

19. Приложения производной: разложение функции в ряд Тейлора и Маклорена. Условия разложимости функции в ряд Тейлора. Разложение в ряд Тейлора основных элементарных функций.

20. Понятие дифференциала функции. Геометрический смысл дифференциала. Применение дифференциала в приближенных вычислениях. Нахождение дифференциалов высших порядков.

21. Экономический смысл производной. Использование производной и ее приложений в экономике и экономической теории.

РАЗДЕЛ 3. Интегральное исчисление функции одной переменной

22. Первообразная функция. Теорема о виде первообразной. Неопределенный интеграл. Свойства неопределенного интеграла. Таблица интегралов от основных элементарных функций.

23. Нахождение неопределенного интеграла методом замены переменной методом интегрирования по частям.

24. Разложение рациональных дробей на простейшие. Метод неопределенных коэффициентов.

25. Интегрирование тригонометрических и некоторых видов иррациональных функций.

26. Понятие определенного интеграла, его геометрический смысл. Достаточное условие существования определенного интеграла. Свойства определенного интеграла. Теорема о среднем.

27. Определенный интеграл как функция верхнего предела. Теоремы о непрерывности функции верхнего предела и производной от нее. Формула Ньютона-Лейбница.

28. Замена переменной и формула интегрирования по частям в определенном интеграле.

29. Геометрические приложения определенного интеграла: площадь плоской фигуры, объем тела вращения.

30. Несобственные интегралы 1-го и 2-го рода. Сходимость и расходимость интегралов. Приближенное вычисление определенных интегралов: формулы прямоугольников, трапеции.

31. Использование понятие определенного интеграла в экономике.

РАЗДЕЛ 4. Функции нескольких переменных

1. Понятие функции нескольких переменных (на примере функции двух переменных). Окрестность точки. График функции. Линии уровня. Предел и непрерывность функции двух переменных.

2. Частные производные. Дифференциал функции двух переменных. Производная по направлению. Градиент функции. Теорема перпендикулярности градиента линии уровня.

3. Экстремум функции двух переменных. Необходимое и достаточное условие экстремума. Схема исследования на экстремум функции двух переменных. Схема нахождения наибольшего и наименьшего значений функции на замкнутом множестве.

4. Условный экстремум. Метод множителей Лагранжа.

5. Двойной интеграл. Его геометрический смысл. Нахождение двойного интеграла повторным интегрированием.

РАЗДЕЛ 5. Обыкновенные дифференциальные уравнения

6. Задачи, приводящие к дифференциальным уравнениям.

7. Дифференциальные уравнения первого порядка. Задача Коши. Теорема существования и единственности решения задачи Коши.

8. Дифференциальные уравнения с разделяющимися переменными. Однородные дифференциальные уравнения.

9. Линейные дифференциальные уравнения 1-го порядка.

10. Линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами. Уравнения с правой частью специального вида.

11. Дифференциальные уравнения высших порядков, допускающие понижение порядка.

РАЗДЕЛ 6. Ряды

12. Числовые ряды. Сходимость и сумма ряда. Необходимое условие сходимости. Действия с рядами.

13. Ряды с неотрицательными членами. Признаки сходимости.

14. Знакопеременные ряды, ряды с комплексными членами. Абсолютная и условная сходимости. Признак Лейбница. Свойства абсолютного сходящихся рядов.

15. Функциональные ряды. Область сходимости. Равномерная сходимость. Признак Вейерштрасса.

16. Свойства равномерно сходящихся рядов: непрерывность суммы ряда, почленное дифференцирование и интегрирование.

17. Степенные ряды. Теорема Абеля. Круг сходимости. Ряды Тейлора и Маклорена. Разложение функций в степенные ряды. Приложение рядов в приближенных вычислениях.

ЛИТЕРАТУРА

1. Высшая математика для экономистов. Учебник для вузов /Под ред. Н.Ш. Кремера. – М: ЮНИТИ–М., 2006-2016.

2. Гусак А.А. Высшая математика. В 2-х т.: Учеб. пособие. Мн: ТетраСистемс, 2006-2016.

3. Шипачев В.С. Высшая математика. М: Высш. шк., 2006-2016.

4. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч.1, 2. М: Высш. шк., 2006-2016.

5. Письменный Д.Т. Конспект лекций по высшей математике. В 2-х т. М: Айрис-пресс, 2006-2016.

6. Натансон И.П. Краткий курс высшей математики. СПб.: Лань, 2006-2016.

7. Ильин В.А., Позняк Э.Г. Математический анализ. М.:ФИЗМАТЛИТ. 2001-2011.

8. Красс М.С., Чупринов Б.П. Основы математики и ее приложения в экономическом образовании. М.: Дело, 2006-2016.

9. Красс М.С. Математика для экономических специальностей. М.:ЮНИТИ–М, 2006-2016.

10. Общий курс высшей математики. Учебник /Под ред. В.И. Ермакова.–М: ИНФРА–М, 2006-2016.

КОНТРОЛЬНАЯ РАБОТА №1

Вариант 1

1. Вычислить пределы:

а)	б)	в)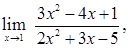
г)	д)	е)

2. Найти производные dy / dx данных функций:

а)	б)
в) ,	г)
д)	е) .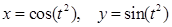

3. Найти наибольшее и наименьшее значения функции 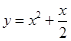на отрезке [–3;3].

4. Исследовать функцию методами дифференциального исчисления и, используя результаты исследования, построить ее график:

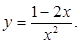
5. Вычислить неопределенные интегралы:

а)	б)
в)	г)
д)	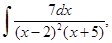е) .

6. Вычислить определенные интегралы:

а)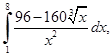

б)

в) .

7. Найти общий или частный интеграл (решение) дифференциального уравнения первого порядка:

а) 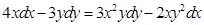,	б) ,
в)	г)
д) 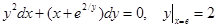,	е)

8. Найти общий или частный интеграл (решение) дифференциального уравнения, допускающего понижения порядка:

а)

б)

9. Найти общее решение неоднородного линейного дифференциального уравнения второго порядка:

а)	б)
в)	г)

10. Найти все частные производные 1-го порядка:

а)

б)

в) .

Вариант 2

1. Вычислить пределы:

а)	б)	в)
г)	д)	е)

2. Найти производные dy / dx данных функций:

а)	б) ,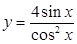
в) ,	г)
д) ,	е) .

3. Найти наибольшее и наименьшее значения функции на отрезке [0;3].

4. Исследовать функцию методами дифференциального исчисления и, используя результаты исследования, построить ее график:

.

5. Вычислить неопределенные интегралы:

а)	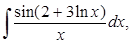б)
в)	г)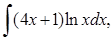
д)	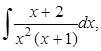е) .

6. Вычислить определенные интегралы:

а)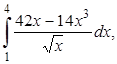

б)

в) .

7. Найти общий или частный интеграл (решение) дифференциального уравнения первого порядка:

а) ,	б) ,
в)	г)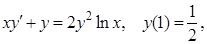
д) ,	е) .

8. Найти общий или частный интеграл (решение) дифференциального уравнения, допускающего понижения порядка:

а)

б) .

9. Найти общее решение неоднородного линейного дифференциального уравнения второго порядка:

а)	в)
б)	г)

10. Найти все частные производные 1-го порядка:

а)

б)

в)

Вариант 3

1. Вычислить пределы:

а)	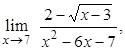б)	в)
г)	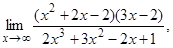д)	е)

2. Найти производные dy / dx данных функций:

а) 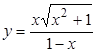,	б) ,
в) ,	г) ,
д) ,	е) .

3. Найти наибольшее и наименьшее значения функции на отрезке [1;4].

4. Исследовать функцию методами дифференциального исчисления и, используя результаты исследования, построить ее график:

.

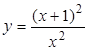5. Вычислить неопределенные интегралы:

а) ,	б) ,
в) ,	г) ,
д) ,	е) .

6. Вычислить определенные интегралы:

а) ,

б) ,

в) .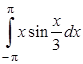

7. Найти общий или частный интеграл (решение) дифференциального уравнения первого порядка:

а) 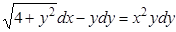,	б) ,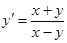
в)	г)
д) ,	е) .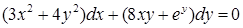

8. Найти общий или частный интеграл (решение) дифференциального уравнения, допускающего понижения порядка:

а)

б)

9. Найти общее решение неоднородного линейного дифференциального уравнения второго порядка:

а)	в)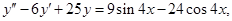
б)	г)

10. Найти все частные производные 1-го порядка:

а) ,

б) ,

в) .

Вариант 4

1. Вычислить пределы:

а)	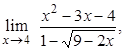б)	в)
г)	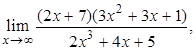д)	е)

2. Найти производные dy / dx данных функций:

а) ,	б) ,
в) ,	г) ,
д) 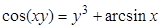,	е) .

3. Найти наибольшее и наименьшее значения функции на отрезке [–3;1].

4. Исследовать функцию методами дифференциального исчисления и, используя результаты исследования, построить ее график:

.

5. Вычислить неопределенные интегралы:

а) ,	б) ,
в)	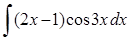г) ,
д) ,	е) .

6. Вычислить определенные интегралы:

а) ,

б) ,

в) .

7. Найти общий или частный интеграл (решение) дифференциального уравнения первого порядка:

а) ,	б) ,
в)	г)
д) ,	е) .

8. Найти общий или частный интеграл (решение) дифференциального уравнения, допускающего понижения порядка:

а)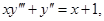

б) .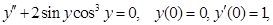

9. Найти общее решение неоднородного линейного дифференциального уравнения второго порядка:

а)	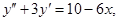в)
б)	г)

10. Найти все частные производные 1-го порядка:

а) ,

б) ,

в) .

Вариант 5

1. Вычислить пределы:

а) ,	б)	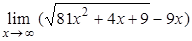в) ,
г) ,	д) ,	е)

2. Найти производные dy / dx данных функций:

а) ,	б) ,
в) ,	г) ,
д) 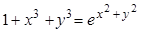,	е) .

3. Найти наибольшее и наименьшее значения функции на отрезке [–6;–1].

4. Исследовать функцию методами дифференциального исчисления и, используя результаты исследования, построить ее график:

Не нашли, что искали? Воспользуйтесь поиском: