
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Программа курса «Математический анализ» Первый семестр 4 страница
4. Исследовать функцию методами дифференциального исчисления и, используя результаты исследования, построить ее график:
 .
.
5. Вычислить неопределенные интегралы:
а)  , ,
| б)  , ,
|
в)  , ,
| г)  , ,
|
д)  , ,
| е)  . .
|
6. Вычислить определенные интегралы:
а)  , ,
| б)  , ,
| в)  . .
|
7. Найти общий или частный интеграл (решение) дифференциального уравнения первого порядка:
а)  , ,
| б)  , ,
|
в) 
| д)  , ,
|
г) 
| е)  . .
|
8. Найти общий или частный интеграл (решение) дифференциального уравнения, допускающего понижения порядка:
а) 
| б)  . .
|
9. Найти общее решение неоднородного линейного дифференциального уравнения второго порядка:
а) 
| в) 
|
б) 
| г) 
|
10. Найти все частные производные 1-го порядка:
а)  , ,
| б)  , ,
| в)  . .
|
Вариант 18
1. Вычислить пределы:
а)  , ,
| б)  , ,
| в)  , ,
|
г)  , ,
| д)  , ,
| е) 
|
2. Найти производные dy / dx данных функций:
а)  , ,
| б)  , ,
|
в)  , ,
| г)  , ,
|
д)  , ,
| е)  . .
|
3. Найти наибольшее и наименьшее значения функции y = x 3–3 x +1 на отрезке [1/2; 2].
4. Исследовать функцию методами дифференциального исчисления и, используя результаты исследования, построить ее график:
 .
.
5. Вычислить неопределенные интегралы:
а)  , ,
| б) 
|
в) 
| г)  , ,
|
д)  , ,
| е)  . .
|
6. Вычислить определенные интегралы:
а)  , ,
| б)  , ,
| в)  . .
|
7. Найти общий или частный интеграл (решение) дифференциального уравнения первого порядка:
а)  , ,
| б)  , ,
|
в) 
| г) 
|
д)  , ,
| е) 
|
8. Найти общий или частный интеграл (решение) дифференциального уравнения, допускающего понижения порядка:
а) 
| б)  . .
|
9. Найти общее решение неоднородного линейного дифференциального уравнения второго порядка:
а) 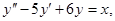
| в) 
|
б) 
| г) 
|
10. Найти все частные производные 1-го порядка:
а)  , ,
| б)  , ,
| в)  . .
|
Вариант 19
1. Вычислить пределы:
а)  , ,
| б)  , ,
| в)  , ,
|
г)  , ,
| д)  , ,
| е) 
|
2. Найти производные dy / dx данных функций:
а)  , ,
| б) 
|
в)  , ,
| г)  , ,
|
д)  , ,
| е)  . .
|
3. Найти наибольшее и наименьшее значения функции y = x 4+4 x на отрезке [–2;2].
4. Исследовать функцию методами дифференциального исчисления и, используя результаты исследования, построить ее график:
 .
.
5. Вычислить неопределенные интегралы:
а)  , ,
| б)  , ,
|
в)  , ,
| г)  , ,
|
д)  , ,
| е)  . .
|
6. Вычислить определенные интегралы:
а) 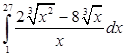 , ,
| б)  , ,
| в)  . .
|
7. Найти общий или частный интеграл (решение) дифференциального уравнения первого порядка:
а)  , ,
| б)  , ,
|
в) 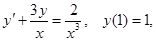
| г) 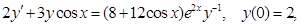
|
д)  , ,
| е) 
|
8. Найти общий или частный интеграл (решение) дифференциального уравнения, допускающего понижения порядка:
а) 
| б)  . .
|
9. Найти общее решение неоднородного линейного дифференциального уравнения второго порядка:
а) 
| в) 
|
б) 
| г)* 
|
10. Найти все частные производные 1-го порядка:
а)  , ,
| б)  , ,
| в)  . .
|
Вариант 20
1. Вычислить пределы:
а)  , ,
| б)  , ,
| в)  , ,
|
г)  , ,
| д)  , ,
| е) 
|
2. Найти производные dy / dx данных функций:
а)  , ,
| б)  , ,
|
в)  , ,
| г)  , ,
|
д)  , ,
| е)  . .
|
3. Найти наибольшее и наименьшее значения функции y = 81 x – x 4 на отрезке [–1;4].
4. Исследовать функцию методами дифференциального исчисления и, используя результаты исследования, построить ее график:
 .
.
5. Вычислить неопределенные интегралы:
а)  , ,
| б)  , ,
|
в)  , ,
| г)  , ,
|
д)  , ,
| е)  . .
|
6. Вычислить определенные интегралы:
а)  , ,
| б)  , ,
| в)  . .
|
7. Найти общий или частный интеграл (решение) дифференциального уравнения первого порядка:
а)  , ,
| б)  , ,
|
в) 
| г) 
|
д) 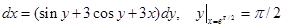 , ,
| е) 
|
8. Найти общий или частный интеграл (решение) дифференциального уравнения, допускающего понижения порядка:
а) 
| б)  . .
|
9. Найти общее решение неоднородного линейного дифференциального уравнения второго порядка:
а) 
| в) 
|
б) 
| г) 
|
10. Найти все частные производные 1-го порядка:
а) 
| б) 
| в) 
|
Вариант 21
1. Вычислить пределы:
а)  , ,
| б)  , ,
| в)  , ,
| |
г)  , ,
| д) 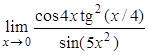 , ,
| е) 
| |
2. Найти производные dy / dx данных функций:
а) 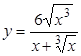 , ,
| б) 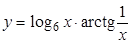 , ,
|
в)  , ,
| г)  , ,
|
д)  , ,
| е) 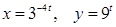 . .
|
3. Найти наибольшее и наименьшее значения функции  на отрезке [0; /2].
на отрезке [0; /2].
4. Исследовать функцию методами дифференциального исчисления и, используя результаты исследования, построить ее график:
 .
.
5. Вычислить неопределенные интегралы:
а)  , ,
| б)  , ,
|
в)  , ,
| г)  , ,
|
д)  , ,
| е) 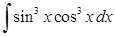 . .
|
6. Вычислить определенные интегралы:
а) 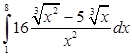 , ,
| б)  , ,
| в) 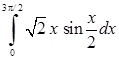 . .
|
7. Найти общий или частный интеграл (решение) дифференциального уравнения первого порядка:
а)  , ,
| б)  , ,
|
в) 
| г) 
|
д)  , ,
| е) 
|
8. Найти общий или частный интеграл (решение) дифференциального уравнения, допускающего понижения порядка:
а) 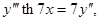
| б)  . .
|
9. Найти общее решение неоднородного линейного дифференциального уравнения второго порядка:
а) 
| в) 
|
б) 
| г)* 
|
10. Найти все частные производные 1-го порядка:
а)  , ,
| б)  , ,
| в)  . .
|
Вариант 22
1. Вычислить пределы:
а)  , ,
| б)  , ,
| в)  , ,
| ||
г)  , ,
| д)  , ,
| е) 
| ||
2. Найти производные dy / dx данных функций:
а)  , ,
| б) 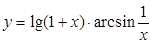 , ,
|
в)  , ,
| г)  , ,
|
д)  , ,
| е)  . .
|
3. Найти наибольшее и наименьшее значения функции y = 3–2 x 2 на отрезке [–1;3].
4. Исследовать функцию методами дифференциального исчисления и, используя результаты исследования, построить ее график:
 .
.
5. Вычислить неопределенные интегралы:
а)  , ,
| б)  , ,
|
в)  , ,
| г)  , ,
|
д)  , ,
| е)  . .
|
6. Вычислить определенные интегралы:
а)  , ,
| б)  , ,
| в) 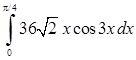 . .
|
7. Найти общий или частный интеграл (решение) дифференциального уравнения первого порядка:
а)  , ,
| б)  , ,
|
в) 
| г) 
|
д)  , ,
| е) 
|
8. Найти общий или частный интеграл (решение) дифференциального уравнения, допускающего понижения порядка:
а) 
| б)  . .
|
9. Найти общее решение неоднородного линейного дифференциального уравнения второго порядка:
а) 
| в) 
|
б) 
| г)* 
|
10. Найти все частные производные 1-го порядка:
а)  , ,
| б)  , ,
| в)  . .
|
Вариант 23
1. Вычислить пределы:
а)  , ,
| б)  , ,
| в)  , ,
|
г)  , ,
| д)  , ,
| е) 
|
2. Найти производные dy / dx данных функций:
Не нашли, что искали? Воспользуйтесь поиском: