
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
КРИВЫЕ ВТОРОГО ПОРЯДКА
Литература: (1, с.135-149; 2, с. 120-138; 3, с. 52-64; 4, с. 52-64)
Определение кривой второго порядка
Кривой второго порядка называется линия, определяемая уравнением второй степени относительно текущих декартовых координат. В общем случае это уравнение имеет вид:
 (18)
(18)
где коэффициент – действительные числа и хотя бы одно из чисел А, В или С отлично от нуля.
К кривым второго порядка относятся линии: окружность, эллипс, гипербола, парабола.
Окружность
Окружностью называется совокупность точек, равноудалённых от одной и той же точки, называется центром. Уравнение окружности имеет вид:
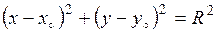 (19)
(19)
где 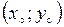 - координаты центра окружности, а
- координаты центра окружности, а  - радиус окружности.
- радиус окружности.
Пример 1. Составить уравнение окружности, которая проходит через точку  и её центр находится в точке
и её центр находится в точке  .
.
Решение. Воспользуемся формулой (19). Имеем  ;
;  . Найдём радиус окружности
. Найдём радиус окружности 
 . Тогда уравнение окружности имеет вид:
. Тогда уравнение окружности имеет вид:

Эллипс
Эллипсом называется совокупность точек, сумма расстояний которых до двух данных точек, называется фокусами, есть величина постоянная. Каноническое (простейшее) уравнение эллипса имеет вид:
 (20)
(20)
где 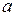 - большая.
- большая. 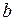 - малая полуоси эллипса (рис. 6)
- малая полуоси эллипса (рис. 6)

 |
 - фокусное расстояние.
- фокусное расстояние.
Связь между 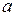 ,
, 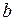 и
и  определяется формулой:
определяется формулой:
 (21)
(21)
Форма эллипса (мера его сжатия) характеризуется эксцентриситетом  :
:
 (22)
(22)
Для эллипса  , так как
, так как  . Фокусы эллипса лежат на большой оси.
. Фокусы эллипса лежат на большой оси.
Пример 2. Составить каноническое уравнение эллипса, проходящего через точки  и
и 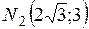 .
.
Решение. Каноническое уравнение эллипса имеет вид (20):  . Так как точки
. Так как точки  и
и  лежат на эллипсе, то их координаты удовлетворяют уравнению (20).
лежат на эллипсе, то их координаты удовлетворяют уравнению (20).
Имеем:

Решая систему получим:  ,
,  . Следовательно, уравнение эллипса имеет вид:
. Следовательно, уравнение эллипса имеет вид: 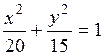 .
.
Гипербола
Гиперболой называется совокупность точек, разность расстояний которых до двух данных точек, называется фокусами, есть величина постоянная.
Каноническое уравнение гиперболы имеет вид:
 (23)
(23)
где 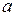 - вещественная,
- вещественная, 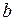 - мнимая полуоси (рис. 7).
- мнимая полуоси (рис. 7).

 - фокусное расстояние. Связь между
- фокусное расстояние. Связь между 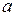 ,
, 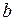 и
и  определяется соотношением:
определяется соотношением:
 (24)
(24)
 Гипербола имеет две асимптоты, уравнения которых:
Гипербола имеет две асимптоты, уравнения которых:
 (25)
(25)
Отношение 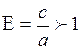 называется эксцентриситетом гиперболы. Фокусы гиперболы расположены на действительной оси.
называется эксцентриситетом гиперболы. Фокусы гиперболы расположены на действительной оси.
Пример 3. Составить каноническое уравнение гиперболы, проходящей через точку  , зная, что её эксцентриситет равен
, зная, что её эксцентриситет равен  .
.
Решение. Такая точка М лежит на гиперболе, то её координаты удовлетворяют уравнению гиперболы. Подставив  ,
,  в уравнение (23), получим
в уравнение (23), получим  . Так как эксцентриситет
. Так как эксцентриситет  , то по условию получим
, то по условию получим  , или
, или 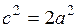 . Используя формулу (24), имеем
. Используя формулу (24), имеем  . Следовательно,
. Следовательно,  . Таким образом, уравнение искомой гиперболы имеет вид
. Таким образом, уравнение искомой гиперболы имеет вид  .
.
Парабола
Параболой называется совокупность точек, равноудалённых от данной точки, называемой фокусом, и данной прямой, называемой директрисой.
Каноническое уравнение параболы:
 (26)
(26)
где 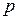 - параметр,
- параметр,  , определяет расстояние от фокуса
, определяет расстояние от фокуса  до директрисы
до директрисы  (рис. 8)
(рис. 8)
 |

Другие виды уравнений параболы (рис. 9)

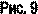 |
Пример 4. Парабола симметрична оси Ох, проходит через точку  , а вершина его лежит в начале координат. Составить её уравнение.
, а вершина его лежит в начале координат. Составить её уравнение.
Решение. Так как парабола проходит через точку  с положительной абсциссой, а её осью служит ось Ох, то уравнение параболы имеет вид
с положительной абсциссой, а её осью служит ось Ох, то уравнение параболы имеет вид  . Подставив координаты тачки А в это уравнение, получим
. Подставив координаты тачки А в это уравнение, получим 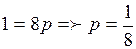 ,
,  . Следовательно, искомое уравнение имеет вид
. Следовательно, искомое уравнение имеет вид  .
.
Не нашли, что искали? Воспользуйтесь поиском: