Преобразование координат

Формулы, выражающие координаты в одной системе через её координаты в другой системе, называются формулами преобразования координат.

Преобразование декартовых координат при параллельном сдвиге осей определяется по формулам:

, (5)

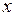где и 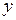- координаты произвольной точки М плоскости относительно старых осей: , - координаты той же точки относительно новых осей; - координаты нового начала старых осей (рис. 3).

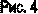Преобразование декартовых прямоугольных координат при повороте осей на угол 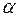(рис. 4) определяется по формулам:

; . (6)

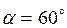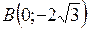Пример 4. Оси координат повёрнуты на угол . Координаты точек и определены в новой системе. Вычислить координаты этих же точек в старой системе координат.

Решение. Воспользуемся формулами (6) ; , где 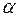- угол поворота, - координаты точек в новой системе, - координаты точки в старой системе.

Тогда для точки А получим:

;

.

Следовательно, .

Аналогично для точки В имеем: ;

. Следовательно, .

Вопросы для самопроверки

Как определяется расстояние между двумя точками?

Как находятся координаты точки, делящей отрезок в данном отношении?

Как задаётся полярная система координат?

Какая существует связь между декартовыми и полярными координатами?

Как определяются параллельный перенос и поворот декартовых прямоугольных осей координат?

Не нашли, что искали? Воспользуйтесь поиском: