
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Простейшие задачи аналитической геометрии
Расстояние между двумя точками 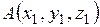 и
и  определяется по формуле:
определяется по формуле:
 (1)
(1)
Деление отрезка в данном отношении
Если точка  лежит на прямой, проходящей через данные точки
лежит на прямой, проходящей через данные точки 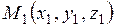 и
и 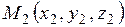 , и делит отрезок
, и делит отрезок  в отношении
в отношении 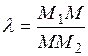 , то координаты точки М определяются по формулам:
, то координаты точки М определяются по формулам:
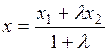 ;
;  ;
; 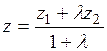 . (2)
. (2)
В частности, если точка  делит отрезок
делит отрезок  пополам, то
пополам, то 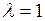 ,
,
 ;
; 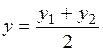 ;
;  .
.
Пример 1. На оси ординат найти точку, равно удалённую от точек  и
и 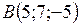 .
.
Решение. Искомая точка М имеет координаты 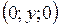 . Найдём её расстояния до точек А и В по формуле (1)
. Найдём её расстояния до точек А и В по формуле (1)
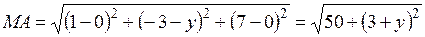 ;
;
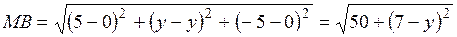 ;
;
По условию  , т.е.
, т.е. 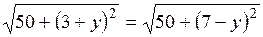 , или
, или  . Итак, искомая точка
. Итак, искомая точка 
Пример 2. Даны вершины треугольника 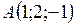 ,
, 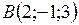 ,
,  . Вычислить длину биссектрисы его внутреннего угла при вершине В.
. Вычислить длину биссектрисы его внутреннего угла при вершине В.
 Решение. Чтобы найти длину биссектрисы
Решение. Чтобы найти длину биссектрисы  нужно знать координаты точки
нужно знать координаты точки  . Воспользуемся тем, что биссектриса делит противоположную сторону на части, пропорциональные прилежащим сторонам, т.е.
. Воспользуемся тем, что биссектриса делит противоположную сторону на части, пропорциональные прилежащим сторонам, т.е.
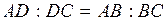
Найдём длинны сторон АВ и ВС по формуле (1):
 ;
;
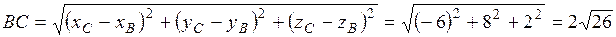 .
.
Тогда.
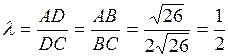
По формуле (2) определим координаты т.  :
:
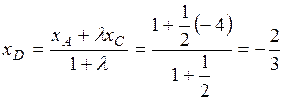 ;
;
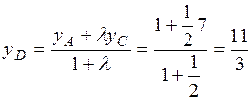 ;
;
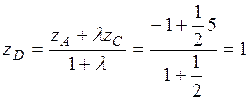 ,
,
 .
.
Следовательно,
 .
.
Не нашли, что искали? Воспользуйтесь поиском: