
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Задачи, решаемые при помощи векторного произведения
1) Нахождение площади параллелограмма, построенного на векторах 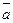 и
и 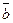 :
:
 (21)
(21)
2) Нахождение момента силы  , приложенной к точке М, относительно точки А:
, приложенной к точке М, относительно точки А:
 (22)
(22)
В этом состоит механический смысл векторного произведения
3) Нахождение синуса угла  между векторами
между векторами 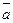 и
и 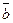 :
:
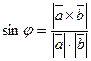 (23)
(23)
Примеры
4.3.1. Векторы 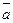 и
и 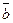 взаимно перпендикулярны. Зная, что
взаимно перпендикулярны. Зная, что  ,
, 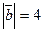 , вычислить
, вычислить  .
.
Решение. Из свойства векторного произведения, раскрывая скобки, получим:

так как  ,
,  ,
,  .
.
4.3.2. Вычислить площадь параллелограмма, построенного на векторах  и
и  .
.
Решение. ПО формуле (21) имеем:  . Так как векторы
. Так как векторы 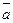 и
и 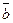 заданы координатами, то найдём векторноё произведение по формуле (20):
заданы координатами, то найдём векторноё произведение по формуле (20):

Следовательно,  .
.
Тогда  .
.
4.3.3. Вычислить площадь треугольника с вершинами  ,
,  ,
,  .
.
Решение. Площадь треугольника АВС равна половине площади параллелограмма, построенного на векторах 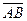 и
и  . Найдём координаты векторов
. Найдём координаты векторов 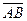 и
и  :
:


Тогда:
 .
.
Следовательно,  .
.
4.3.4. Даны три силы приложенные к точке  :
:
 ;
;  ;
; 
Найти момент их равнодействующей относительно точки  .
.
Решение. Воспользуемся формулой (22): 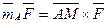
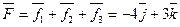 ;
;
 .
.
Тогда:
 .
.
Вопросы для самопроверки
Что называется векторным произведением векторов? Как оно обозначается?
Какими свойствами обладает векторное произведение?
Каков геометрический смысл векторного произведения?
Каков механический смысл векторного произведения?
Как считаются векторные произведения основных ортов?
Как находится векторное произведение векторов, заданных своими координатами?
Какие задачи решаются при помощи векторного произведения?
Не нашли, что искали? Воспользуйтесь поиском: