Определение и свойство векторного произведения векторов

Векторным произведением вектора 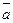на вектор 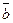называется такой вектор , который удовлетворяет следующим условиям:

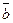1) , где - угол между векторами и .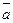

2) Вектор перпендикулярен к каждому из векторов 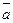и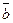

3) Направлен вектор так, что кратчайший поворот от 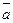к 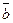виден из конца вектора против часовой стрелки.

Векторное произведение вектора 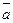на вектор 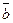обозначается через .

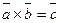Свойства векторного произведения:

1) , т.е. векторное произведение не обладает переместительными свойством.

2) , если , либо , либо . В частности, .

3)

4) .

5) Есл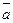и и 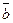неколлинеарны, то модуль векторного произведения равен площади построенного на них параллелограмма (геометрический смысл). Векторные произведения координатных ортов:

; ;

Векторное произведение векторов заданных своими координатами определяется по формуле:

(20)

Не нашли, что искали? Воспользуйтесь поиском: