
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Действия над векторами, заданными координатами
Равные вектора имеют равные координаты.
Вектор  , направленный из начала координат в точку
, направленный из начала координат в точку  , называется радиусом – вектором точки
, называется радиусом – вектором точки  . Проекции радиуса-вектора равны координаты точки М, т.е.
. Проекции радиуса-вектора равны координаты точки М, т.е.
 (4)
(4)
Если даны координаты точек 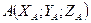 и
и  , то координаты вектора
, то координаты вектора 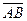 получаются вычитанием из координат его конца В координат начала А:
получаются вычитанием из координат его конца В координат начала А:
 (5)
(5)
При сложении (вычитании) векторов их координаты складываются (вычитаются); при умножении вектора на число все го координаты умножаются на это число, т.е. если  ,
,  , то
, то
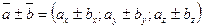 (6)
(6)
 (7)
(7)
Если векторы 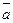 и
и 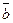 коллинеарные, то
коллинеарные, то  и, следовательно,
и, следовательно,
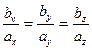 (8)
(8)
Формула (8) выражает условие коллинеарности двух векторов: для того, чтобы два вектора были коллинеарны, необходимо и достаточно, чтобы их проекции были пропорциональны.
Не нашли, что искали? Воспользуйтесь поиском: