Канонические уравнения прямой

Пусть прямая проходит через точку параллельно вектору 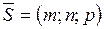. Всякий вектор 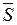, параллельный прямой, называется направляющим вектором прямой.

Канонические уравнения прямой имеют вид:

(36)

Чтобы перейти от общих уравнений прямой к каноническим, необходимо:

1) найти какую-либо точку . Для этого следует задать числовое значение одной из неизвестных координат точки и подставить его вместо соответствующей переменной в уравнения (35), после этого две другие координаты определяются в результате совместного решения уравнения (35);

2) найти направляющий вектор 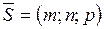. В качестве вектора 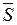можно взять любой вектор, перпендикулярный векторам и , например их векторное произведение .

Пример 1. Найти канонические уравнения прямой и .

Решение. Выберем произвольную точку на прямой, пологая, например, .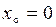

Получим:

Решая эту систему, найдём , . За направляющий вектор прямой примем векторное произведение векторов и :

Следовательно, искомая прямая определяется уравнением

Не нашли, что искали? Воспользуйтесь поиском: