Прямая и плоскость в пространстве. Угол между прямой и плоскостью

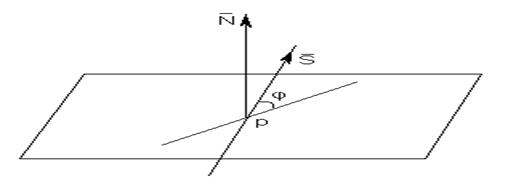Углом между прямой и плоскостью называется угол между прямой и её проекцией на эту плоскость (рис. 14).

Этот угол определяется по формуле:

(41)

Условие параллельности прямой и плоскости:

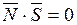, т.е. 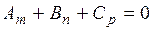(42)

Условие перпендикулярности:

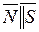, т.е. 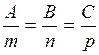(43)

Пример 4. Найти угол между прямой и плоскостью .

Решение. Найдём направляющий вектор прямой:

Из уравнения плоскости заключаем, что нормальный вектор плоскости 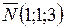. Тогда по формуле (41) имеем:

;

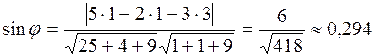Пример 5. Найти точку пересечения прямой и плоскости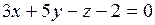

Решение. Приведём уравнение прямой к параметрическому виду, приравнивая к 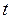каждоё из трёх данных отношений:

, ,

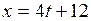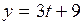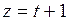
Подставляя в уравнение плоскости, получим значение параметра 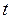, отвечающее точке пересечения:

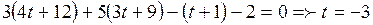
Искомая точка пересечения прямой и плоскости имеет координаты:

; ; .

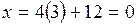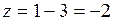Пример 6. Составить уравнение плоскости, проходящей через две параллельные прямые

, .

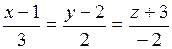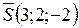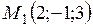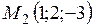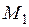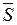Решение. Так как две прямые лежат в плоскости, то в ней лежат вектора - направляющий и , соединяющий точки и . Взяв текущую точку плоскости и соединив её с одной из точек, например, получим вектор , принадлежащий плоскости. Следовательно, векторы , и 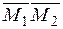компланарны, т.е. 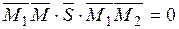. Получим:

.

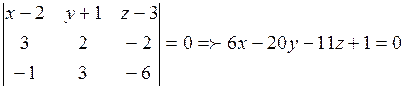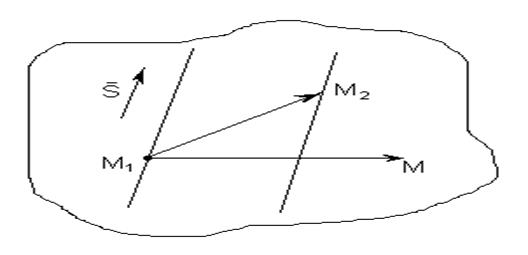
Для наглядности полезно сделать рис. 15.

Вопросы для самопроверки

Как определяются общее уравнения прямой?

Какие уравнения прямой называются каноническими? Что называется направляющим вектором прямой?

Как перейти от общих уравнений прямой к каноническим?

Как записываются параметрические уравнения прямой?

Как определяется угол между прямыми? Сформулируйте условия параллельности и перпендикулярности между прямой и плоскостью.

Не нашли, что искали? Воспользуйтесь поиском: