
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
Единичные показатели надежности объектов характеризуют какое-либо одно ее свойство: безотказность, долговечность, ремонтопригодность, сохраняемость. Объект в процессе хранения и эксплуатации может находиться или в работоспособном, или в неработоспособном состоянии. Время пребывания объекта в любом из этих состояний является непрерывной случайной величиной.
Математическое описание случайных величин в теории надежности осуществляется методами теории вероятностей и математической статистики. Универсальной вероятностной характеристикой случайной величины является закон ее распределения. Используются также числовые характеристики случайной величины, выражающие наиболее существенные особенности ее распределения. Статистическая опенка единичных показателей безотказности и долговечности проводится на основе модели эксплуатации (испытания) невосстанавливаемых объектов. Далее рассматриваются единичные показатели надежности и их связь с характеристиками случайных величин.
Единичные показатели надежности и их связь с характеристиками случайных величин приведены в табл. 1.
Модель эксплуатации невосстанавливаемых объектов (модель испытания объектов на долговечность) используется для определения вероятностных характеристик ресурса и срока службы электротехнических объектов, а также наработки до первого отказа. Статистическая информация об отказах получается из наблюдений за эксплуатацией или испытаниями в заданных условиях  одинаковых объектов. Каждый объект работает от начала его эксплуатации до первого отказа и после отказа не восстанавливается и не заменяется работоспособным. Испытания считаются законченными после отказа всех объектов. При этом определяются наработки каждого объекта от начала его эксплуатации до первого отказа и записываются в виде вариационного ряда, т. е.
одинаковых объектов. Каждый объект работает от начала его эксплуатации до первого отказа и после отказа не восстанавливается и не заменяется работоспособным. Испытания считаются законченными после отказа всех объектов. При этом определяются наработки каждого объекта от начала его эксплуатации до первого отказа и записываются в виде вариационного ряда, т. е. 
Закон распределения случайной величины является ее универсальной вероятностной характеристикой. В рассматриваемой модели эксплуатации случайным событием является отказ объекта, а случайной величиной - ресурс, наработка объекта от начала эксплуатации до перехода в предельное состояние. Случайные события будут полностью описаны с вероятностной точки зрения, если задать распределение вероятностей соответствующих им случайных величин.
Законом распределения вероятностей случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Закон распределения имеет разные формы: ряд распределения, интегральная функция распределения и дифференциальная функция распределения.
| Термины теории вероятности | Безотказность | Долговечность | Ремонтопригодность | Сохраняемость | |
| Случайная величина | Наработка* | Ресурс* 
| Срок службы* 
| Время восстановления 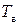
| Срок сохраняемости* 
|
| Интегральная функция распределения вероятностей случайной величины | Вероятность отказа 
| − | − | Функция распределения времени восстановления 
| − |
| Дополнение интегральной функции распределения вероятностей случайной величины | Вероятность безотказной работы* 
| − | − | Вероятность восстановления * 
| Вероятность невозникновения отказа |
| Дифференциальная функция распределения вероятностей случайной величины | Плотность распределения наработки 
| Плотность распределения ресурса 
| Плотность распределения срока службы 
| Плотность распределения времени восстановления 
| Плотность распределения срока сохраняемости 
|
| Интенсивность событий | Интенсивность отказов* 
| − | − | Интенсивность восстановлений 
| − |
| Математическое ожидание случайной величины | Наработка до отказа средняя* 
| Ресурс средний* 
| Срок службы средний* 
| Время восстановления среднее* 
| Срок сохраняемости средний* 
|
| − | Наработка до отказа гамма-процентная* | Ресурс гамма-процентный* 
| Срок службы гамма-процентный* 
| − | Срок сохраняемости гамма-процентный* 
|
| Медиана случайной величины | − | Ресурс медианный 
| Срок службы медианный 
| − | Срок сохраняемости медианный 
|
| − | − | Ресурс до первого капитального ремонта 
| Срок службы до первого капитального ремонта 
| − | − |
| − | − | Ресурс межремонтный 
| Срок службы межремонтный 
| − | − |
| − | − | Ресурс суммарный | Срок службы до списания | − | − |
| − | − | Наработка гарантийная | Срок гарантии | − | − |
| − | − | Ресурс назначенный* 
| Срок службы назначенный* | − | − |
| *Термины установлены ГОСТ 27.002−83 |
Интегральная функция распределения вероятностей случайной величины является одной из форм закона распределения. Наибольшее распространение в прикладных задачах теории вероятностей, теории массового обслуживания, теории надежности и т. д. имеют события вида  , состоящие в том, что случайная величина
, состоящие в том, что случайная величина  примет значение, меньшее некоторого действительного числа
примет значение, меньшее некоторого действительного числа  . Вероятность
. Вероятность  события
события  изменяется при изменении действительного числа
изменяется при изменении действительного числа  . Рассматривая действительное число
. Рассматривая действительное число  как независимую переменную, получают интегральную функцию распределения вероятностей случайной величины.
как независимую переменную, получают интегральную функцию распределения вероятностей случайной величины.
Интегральной функцией распределения вероятностей случайной величины  называется функция
называется функция  , определяющая для каждого значения аргумента
, определяющая для каждого значения аргумента  : вероятность события
: вероятность события  , состоящего в том, что случайная величина
, состоящего в том, что случайная величина  примет значение, меньшее
примет значение, меньшее  , т. е.
, т. е.  .
.
Геометрически это означает, что  есть вероятность того, что случайная величина
есть вероятность того, что случайная величина  примет значение, которое изображается на числовой оси точкой, расположенной левее точки
примет значение, которое изображается на числовой оси точкой, расположенной левее точки  .
.
Интегральная функция  , как всякая вероятность, есть величина безразмерная. Интегральная функция полностью характеризует случайную величину с вероятностной точки зрения. Интегральная функция является самой универсальной характеристикой случайной величины, так как существует как для дискретных, так и для непрерывных случайных величин. Для краткости часто используются термины: интегральная функция распределения, интегральная функция, функция распределения.
, как всякая вероятность, есть величина безразмерная. Интегральная функция полностью характеризует случайную величину с вероятностной точки зрения. Интегральная функция является самой универсальной характеристикой случайной величины, так как существует как для дискретных, так и для непрерывных случайных величин. Для краткости часто используются термины: интегральная функция распределения, интегральная функция, функция распределения.
Дополнение интегральной функции распределения вероятностей случайной величины  определяет вероятность противоположного события
определяет вероятность противоположного события  . Дополнением интегральной функции распределения вероятностей случайной величины
. Дополнением интегральной функции распределения вероятностей случайной величины  называется функция
называется функция 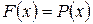 , определяющая для каждого значения аргумента
, определяющая для каждого значения аргумента  вероятность события
вероятность события  , состоящего в том, что случайная величина
, состоящего в том, что случайная величина  примет значение, большее
примет значение, большее  , т. е.
, т. е.
 . (1)
. (1)
Геометрически это означает, что  есть вероятность того, что случайная величина
есть вероятность того, что случайная величина  примет значение, которое изображается на числовой оси точкой, расположенной правее точки
примет значение, которое изображается на числовой оси точкой, расположенной правее точки  .
.
События  и
и  (например, отказ и отсутствие отказа объекта) - случайные несовместные противоположные события, образующие полную группу. Сумма вероятностей событий, образующих полную группу, равна единице, т. е.
(например, отказ и отсутствие отказа объекта) - случайные несовместные противоположные события, образующие полную группу. Сумма вероятностей событий, образующих полную группу, равна единице, т. е.
 . (2)
. (2)
Это уравнение позволяет определить одну из этих функций по известной другой.
Интегральная функция распределения, и ее дополнение в теории надежности характеризуют различные случайные величины: время работы объекта до отказа, ресурс и срок службы объекта, время восстановления работоспособности объекта, срок сохраняемости объекта.
Свойства интегральной функции распределения состоят в следующем:
· интегральная функция изменяется в пределах  , так как вероятность всегда неотрицательное число, не превышающее единицы;
, так как вероятность всегда неотрицательное число, не превышающее единицы;
· интегральная функция не убывает, т. е.  , если
, если  .
.
Вероятность попадания случайной величины  на интервал
на интервал  ,
,  равна приращению интегральной функции на этом интервале (рис. 8, а)
равна приращению интегральной функции на этом интервале (рис. 8, а)
 . (3)
. (3)


а) б)


в) г)
Рис. 10. Определение вероятности попадания
случайной величины в заданный интервал
Вероятность любого определенного значения непрерывной случайной величины, например  , равна нулю
, равна нулю  .
.
Если все возможные значения случайной величины принадлежат интервалу  ,
,  , то
, то
 и
и  . (4)
. (4)
Вероятность отказа объекта - функция  , определяющая для каждого значения времени
, определяющая для каждого значения времени  вероятность события
вероятность события  , состоящего в том, что время
, состоящего в том, что время  работы объекта до отказа примет значение, меньшее
работы объекта до отказа примет значение, меньшее  , т. е.
, т. е.
 . (5)
. (5)
Функция (5) является интегральной функцией распределения вероятностей времени работы объекта до отказа, определяющей вероятность возникновения отказа объекта в интервале времени  .
.
Вероятность  отказа по статистической информации определяется как отношение числа объектов, отказавших за время
отказа по статистической информации определяется как отношение числа объектов, отказавших за время  , к числу объектов в начале испытания по формуле
, к числу объектов в начале испытания по формуле
 (6)
(6)
где  - число объектов, отказавших за время
- число объектов, отказавших за время  ;
;  - число объектов, работоспособных в момент времени
- число объектов, работоспособных в момент времени  ;
;  - число объектов в начале испытания;
- число объектов в начале испытания;  - вероятность безотказной работы.
- вероятность безотказной работы.
Вероятность безотказной работы объекта - функция  , определяющая для каждого значения времени
, определяющая для каждого значения времени  вероятность события
вероятность события  , состоящего в том, что время Т работы объекта до отказа примет значение, большее
, состоящего в том, что время Т работы объекта до отказа примет значение, большее  , т. е.
, т. е.
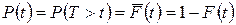 . (7)
. (7)
Функция (7) является дополнением интегральной функции распределения вероятностей времени безотказной работы объекта, определяющей вероятность безотказной работы объекта в интервале времени  .
.
Вероятность  безотказной работы по статистической информации определяется как отношение числа объектов, работоспособных в момент времени
безотказной работы по статистической информации определяется как отношение числа объектов, работоспособных в момент времени  , к числу объектов в начале испытания по формуле
, к числу объектов в начале испытания по формуле
 . (8)
. (8)
Вероятность восстановления работоспособности объекта - функция  , определяющая для каждого значения времени
, определяющая для каждого значения времени  вероятность события
вероятность события  , состоящего в том, что время
, состоящего в том, что время  восстановления работоспособности примет значение, меньшее
восстановления работоспособности примет значение, меньшее  , т. е.
, т. е.
 . (9)
. (9)
Функция (9) является интегральной функцией распределения вероятностей времени восстановления работоспособности объекта, определяющей вероятность восстановления работоспособности в интервале времени  .
.
Дифференциальная функция распределения вероятностей случайной величины является первой производной от интегральной функции распределения
 . (10)
. (10)
Продифференцировав выражение (2), получим
 . (11)
. (11)
Геометрически дифференциальная функция как производная интегральной функции определяет тангенс угла между осью абсцисс и касательной к интегральной функции в дайной ее точке. Размерность дифференциальной функции, как это видно из формулы (10), обратная размерности случайной величины.
Дифференциальная функция так же, как и интегральная функция, является одной из форм закона распределения. Часто вместо термина «дифференциальная функция распределения» пользуются терминами «плотность распределения» или «плотность вероятности», которые следуют из представления о том, что дифференциальная функция характеризует как бы плотность, с которой распределяются значения случайной величины в данной точке. Эти термины становятся особенно наглядными при механической интерпретации, в которой дифференциальная функция характеризует линейную плотность распределения масс по оси абсцисс.
Частота появления событий является вероятностью их появления в единицу времени. Непрерывные случайные величины в теории надежности связаны с событиями, в результате которых случайная величина приняла то или иное случайное значение. Дифференциальная функция (плотность распределения) с этой точки зрения определяет вероятность появления событий в единицу времени, которая может быть интерпретирована как частота появления событий, например частота отказов объектов, частота восстановлений работоспособности объектов.
Частота отказов (плотность распределения времени работы объекта до отказа) по статистической информации определяется как отношение числа объектов, отказавшись в единицу времени, к числу объектов в начале испытания по формуле
 , (12)
, (12)
где  - интервал времени от
- интервал времени от  до
до  ;
;  - число объектов, отказавших в интервале времени
- число объектов, отказавших в интервале времени  ;
;  - число объектов, отказавших за время
- число объектов, отказавших за время  ;
;  - число объектов в начале испытания.
- число объектов в начале испытания.
График дифференциальной функции распределения вероятностей случайной величины, построенный по статистической информации, называют гистограммой (рис. 9). Для ее построения разбивают весь диапазон возможных значений непрерывной случайной величины на интервалы  обычной равной длины и для каждого интервала определяют по формуле (12) значения
обычной равной длины и для каждого интервала определяют по формуле (12) значения  , которые откладывают по оси ординат. В результате получается приближенное представление кривой дифференциальной функции распределения вероятностей в виде ступенчатой линии. При одинаковых масштабах площади столбиков гистограммы приблизительно равны площадям соответствующих криволинейных трапеций под кривой дифференциальной функции распределения вероятностей. Разумеется, что для хорошего приближения необходимо, чтобы в каждый интервал попало достаточно много эмпирических точек.
, которые откладывают по оси ординат. В результате получается приближенное представление кривой дифференциальной функции распределения вероятностей в виде ступенчатой линии. При одинаковых масштабах площади столбиков гистограммы приблизительно равны площадям соответствующих криволинейных трапеций под кривой дифференциальной функции распределения вероятностей. Разумеется, что для хорошего приближения необходимо, чтобы в каждый интервал попало достаточно много эмпирических точек.

Рис. 9 Гистограмма
Вероятность попадания непрерывной случайной величины в заданный интервал  выраженная через дифференциальную функцию, определяется интегрированием выражения (10) в пределах от
выраженная через дифференциальную функцию, определяется интегрированием выражения (10) в пределах от  до
до  с учетом формулы (3)
с учетом формулы (3)
 , (13)
, (13)
т. е. вероятность попадания непрерывной случайной величины  в заданный интервал
в заданный интервал  равна определенному интегралу от дифференциальной функции в пределах от
равна определенному интегралу от дифференциальной функции в пределах от  до
до  .
.
Геометрически вероятность попадания непрерывной случайной величины  в интервал
в интервал  равна площади криволинейной трапеции, ограниченной осью абсцисс, графиком дифференциальной функции
равна площади криволинейной трапеции, ограниченной осью абсцисс, графиком дифференциальной функции  и прямыми
и прямыми 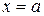 и
и  (см. рис. 8, б).
(см. рис. 8, б).
Вероятность появления случайного события (отказа объекта, восстановления работоспособности объекта) на интервале  равна вероятности (13) попадания соответствующей ему случайной величины
равна вероятности (13) попадания соответствующей ему случайной величины  (времени безотказной работы объекта, времени восстановления работоспособности объекта) в этот интервал.
(времени безотказной работы объекта, времени восстановления работоспособности объекта) в этот интервал.
Свойства дифференциальной функции распределения заключаются в следующем:
1. дифференциальная функция неотрицательна, т. е.  , так как производная неубывающей функции неотрицательна;
, так как производная неубывающей функции неотрицательна;
2. интеграл от дифференциальной функции в пределах области существования всех возможных значений случайной величины от  до
до  равен единице
равен единице
 . (14)
. (14)
Интеграл (14) выражает вероятность события, состоящего в том, что случайная величина примет значение, принадлежащее интервалу  , в котором заключены все ее возможные значения. Такое событие достоверно, и, следовательно, вероятность его равна единице.
, в котором заключены все ее возможные значения. Такое событие достоверно, и, следовательно, вероятность его равна единице.
Геометрически это означает, что вся площадь криволинейной трапеции, ограниченной осью  и графиком дифференциальной функции (кривой распределения), равна единице. В частности, несобственный интеграл от дифференциальной функции в пределах от
и графиком дифференциальной функции (кривой распределения), равна единице. В частности, несобственный интеграл от дифференциальной функции в пределах от  до
до  также равен единице, если все возможные значения случайной величины принадлежат интервалу
также равен единице, если все возможные значения случайной величины принадлежат интервалу  .
.
Определение интегральной функции распределения по известной дифференциальной функции производится интегрированием формулы (10):
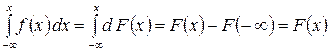 . (15)
. (15)
Геометрически интегральная функция  ровна площади криволинейной трапеции, ограниченной осью
ровна площади криволинейной трапеции, ограниченной осью  и графиком дифференциальной функции
и графиком дифференциальной функции  , правее точки
, правее точки  (см. рис. 8, в).
(см. рис. 8, в).
Дополнение интегральной функции по (2) и (15) равно
 . (16)
. (16)
Геометрически дополнение интегральной функции  равно площади криволинейной трапеции, ограниченной осью
равно площади криволинейной трапеции, ограниченной осью  и графиком дифференциальной функции
и графиком дифференциальной функции  , правее точки
, правее точки  (см. рис. 8, г).
(см. рис. 8, г).
Вероятность появления события на интервале, следующем за интервалом, на котором событие не появлялось, является условной вероятностью. Для ее определения найдем сначала условную вероятность  непоявления события на интервале
непоявления события на интервале  при условии непоявления события па предыдущем интервале
при условии непоявления события па предыдущем интервале  (рис. 10). По теореме умножения вероятностей зависимых событий можно записать
(рис. 10). По теореме умножения вероятностей зависимых событий можно записать
 , (17)
, (17)
где  - безусловная вероятность непоявления события на интервале
- безусловная вероятность непоявления события на интервале  ;
; 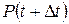 - безусловная вероятность непоявления события на интервале
- безусловная вероятность непоявления события на интервале  , т. е. вероятность одновременного не появления события и на интервале
, т. е. вероятность одновременного не появления события и на интервале  , и на интервале
, и на интервале  .
.

Рис. 10. Определение условной вероятности события на интервале времени
Вероятность  не появления события (отказа, восстановления работоспособности изделия) на интервале
не появления события (отказа, восстановления работоспособности изделия) на интервале  при условии непоявления события на предыдущем интервале
при условии непоявления события на предыдущем интервале  из формулы (17) равна
из формулы (17) равна
 , (18)
, (18)
т. е. равна отношению вероятностей непоявления события в конце и в начале рассматриваемого интервала времени  .
.
Вероятность  появления события (отказа, восстановления работоспособности) на интервале
появления события (отказа, восстановления работоспособности) на интервале  при условии непоявления события на предыдущем интервале
при условии непоявления события на предыдущем интервале  из формул (2) и (18) равна
из формул (2) и (18) равна
 . (19)
. (19)
Интенсивность событий (отказов, восстановлений работоспособности) - функции,  определяющая вероятность появления события в единицу времени в момент
определяющая вероятность появления события в единицу времени в момент  при условии, что событие не появилось до момента
при условии, что событие не появилось до момента  . Интенсивность событий является плотностью вероятности появления события в момент времени
. Интенсивность событий является плотностью вероятности появления события в момент времени  при условии, что событие не появлялось до момента
при условии, что событие не появлялось до момента  .
.
Условная вероятность появления события в единицу времени на интервале  из формулы (19) равна
из формулы (19) равна
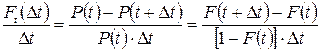 . (20)
. (20)
Интенсивность событий (отказов, восстановлений работоспособности) получается в результате перехода в этом уравнении к пределу при 
 . (21)
. (21)
Интенсивность отказов по статистической информации определяется как отношение числа объектов, отказавших в единицу времени, к числу объектов, работоспособных в данный момент времени,
 , (22)
, (22)
где  - интервал времени от
- интервал времени от  до
до  ;
;  - число объектов, отказавших в интервале времени
- число объектов, отказавших в интервале времени  ;
;  - число объектов, работоспособных в момент времени
- число объектов, работоспособных в момент времени  .
.
Интенсивность отказов - удобный показатель безотказности элементов, так как позволяет более просто вычислять показатели безотказности системы.
Определение вероятности появления событий через их интенсивность производится интегрированием (21). Из уравнения (21) имеем
 . (23)
. (23)
Интегрируем это выражение
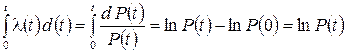 , (24)
, (24)
откуда
 . (25)
. (25)
Не нашли, что искали? Воспользуйтесь поиском: