ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН

Числовые характеристики случайных величин широко применяются на практике расчета показателей надежности. Во многих вопросах практики нет необходимости полностью, исчерпывающим образом характеризовать случайную величину. Зачастую бывает достаточно указать только числовые параметры, до некоторой степени характеризующие существенные черты распределения случайной величины, например: среднее значение, около которого группируются возможные значения случайной величины; число, характеризующее рассеяние случайной величины относительно среднего значения, и т. д. Числовые параметры, позволяющие в сжатой форме выразить наиболее существенные особенности случайной величины, называются числовыми характеристиками случайной величины.

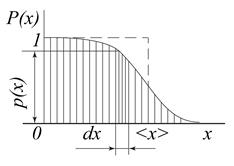
а) б)

Рис. 11 Определение математического ожидания

Числовые характеристики случайных величин, применяемые в теории надежности, приведены в табл. 1.

Математическое ожидание (среднее значение) непрерывной случайной величины , возможные значения которой принадлежат интервалу , представляет собой определенный интеграл (рис., 11, б)

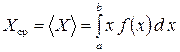. (26)

Математическое ожидание можно выразить через дополнение интегральной функции. Для этого подставим (11) в (26) и проинтегрируем по частям полученное выражение

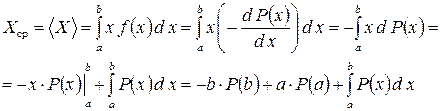, (27)

так как 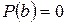и , то

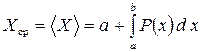. (28)

Для неотрицательных случайных величин, возможные значения которых принадлежат интервалу , формула (28) принимает вид

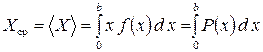. (29)

т. е. математическое ожидание неотрицательной случайной величины, возможные значения которой принадлежат интервалу , численно равно площади под графиком дополнения интегральной функции (рис., 11, а).

Средняя наработка до первого отказа по статистической информации определяется по формуле

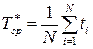, (30)

где 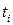- наработка до первого отказа i -го объекта; N - число испытываемых объектов.

Аналогично определяется средний ресурс, средний срок службы, среднее время восстановления работоспособности, средний срок сохраняемости.

Рассеивание случайной величины около ее математического ожидания оценивается с помощью дисперсии среднего квадратического отклонения (СКО) и коэффициента вариации.

Дисперсия непрерывной случайной величины X представляет собой математическое ожидание квадрата отклонения случайной величины от ее математического ожидания и вычисляется по формуле

. (31)

Дисперсия имеет размерность квадрата случайной величины, что не всегда удобно.

Среднее квадратическое отклонение случайной величины является квадратным корнем из дисперсии и имеет размерность случайной величины

. (32)

Коэффициент вариации является относительным показателем рассеивания случайной величины и определяется как отношение среднего квадратического отклонения к математическому ожиданию

. (33)

Гамма - процентное значение случайной величины - значение 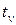случайной величины , соответствующее заданной вероятности того, что случайная величина примет значение, большее ,

. (34)

Гамма - процентное значение случайной величины можно определить по интегральной функции, ее дополнению и дифференциальной функции (рис. 12). Гамма-процентное значение случайной величины является квантилем вероятности (рис. 12, а)

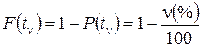. (35)

В теории надежности используется гамма-процентное значение ресурса, срока службы и срока сохраняемости (табл. 1). Гамма-процентным называется ресурс, срок службы, срок сохраняемости, который имеет (и превышает) процентов объектов данного типа.

а) б)

в)

Рис.12 Определение гамма-процентного значения случайной величины

Гамма-процентный ресурс характеризует долговечность при выбранном уровне вероятности неразрушения. Гамма-процентный ресурс назначается с учетом ответственности объектов. Например, для подшипников качения наиболее часто используют 90-процентный ресурс, для подшипников наиболее ответственных объектов выбирают 95-процентный ресурс и выше, приближая его к 100-процентному, если отказ опасен для жизни людей.

Медиана случайной величины является ее гамма- процентным значением при 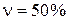. Для медианы одинаково вероятно, окажется ли случайная величина Т больше или меньше ее, т. е. .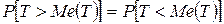

Геометрически медиана является абсциссой точки пересечения интегральной функции распределения и ее дополнения (рис. 12, б). Медиану можно истолковать как абсциссу точки, в которой ордината дифференциальной функции делит пополам площадь, ограниченную кривой распределения (рис., 12, в).

Медиана случайной величины используется в теории надежности как числовая характеристика ресурса, срока службы, срока сохраняемости (табл. 1).

Между показателями надежности объектов существует функциональная связь. Знание одной из функций 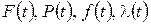позволяет определить другие показатели надежности. Сводка соотношений между показателями надежности приведена в табл. 2.

Таблица 2. Функциональная связь между показателями надежности

Показатели

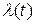
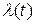
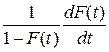
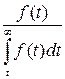
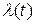
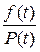
Не нашли, что искали? Воспользуйтесь поиском: