
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Основные определения устойчивости по Ляпунову решений динамических систем (систем обыкновенных дифференциальных уравнений)
А. М. Ляпунов (1857-1918) - знаменитый русский математик и механик, основатель метода функций Ляпунова – основного математического метода исследования устойчивости решений нелинейных и нестационарных, в общем случае, систем обыкновенных дифференциальных уравнений.
Пусть дана конечномерная гладкая динамическая система с непрерывным временем, т.е. система обыкновенных дифференциальных уравнений (1.1.7) вида:
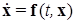 (1.2.1)
(1.2.1)
с областью определения (1.1.8) вида
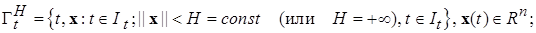 (1.2.2)
(1.2.2)
и вектор-функция 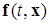 удовлетворяет условиям (1.1.9) единственности области
удовлетворяет условиям (1.1.9) единственности области  .
.
Пусть также дано некоторое известное фиксированное решение системы (1.2.1) вида
 (1.2.3)
(1.2.3)
из области единственности, т.е. с начальными данными  вида (1.2.2).
вида (1.2.2).
Отметим, что во втором методе Ляпунова исследуются только отдельные фиксированные решения (1.2.3) нелинейных нестационарных систем (1.2.1) в области единственности (1.2.2).
Определение 1 (устойчивости по Ляпунову). Решение  системы (1.2.1) называется устойчивым по Ляпунову при
системы (1.2.1) называется устойчивым по Ляпунову при  (или, короче, устойчивым), если для любого наперед заданного положительного числа
(или, короче, устойчивым), если для любого наперед заданного положительного числа 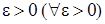 и любого начального момента времени
и любого начального момента времени  существует (найдется) положительное число
существует (найдется) положительное число 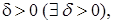 выбор которого, в общем случае, зависит от выбора
выбор которого, в общем случае, зависит от выбора 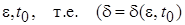 , такое, что все решения
, такое, что все решения 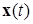 системы (1.2.1), удовлетворяющие (строгому) неравенству
системы (1.2.1), удовлетворяющие (строгому) неравенству
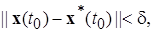 (1.2.4)
(1.2.4)
обладают следующими свойствами:
a) они бесконечно продолжимы вправо, включая и фиксированное решение 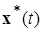 ; т.е. все они определены на
; т.е. все они определены на 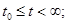
б) для этих решений справедливо (строгое) неравенство
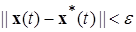 (1.2.5)
(1.2.5)
при всех t из полубесконечного интервала времени 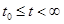 .■
.■
Замечание. Отметим некоторые характерные черты устойчивого по Ляпунову решения, вытекающие из данного определения.
1. Неравенства (1.2.4), (1.2.5) означают, что все решения x (t), которые начинаются, согласно неравенству (1.2.4), внутри некоторой окрестности  открытого шара радиуса
открытого шара радиуса 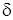 , т.е. «достаточно близкие» к решению
, т.е. «достаточно близкие» к решению 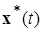 в любой начальный момент времени
в любой начальный момент времени 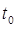 , целиком погружаются, согласно неравенству (1.2.5), в сколь угодно узкую
, целиком погружаются, согласно неравенству (1.2.5), в сколь угодно узкую 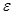 -трубку, построенную вокруг решения
-трубку, построенную вокруг решения 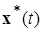 (см. рисунок 1).
(см. рисунок 1).

Рисунок 1.
2. Из неравенств (1.2.4), (1.2.5) по смыслу вытекает, что всегда можно выбрать  (без потери общности).
(без потери общности).
3. Пусть фиксированное решение системы (1.2.1)  ограничено по норме, т.е. для всех
ограничено по норме, т.е. для всех 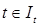 найдется число
найдется число 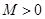 такое, что
такое, что 

Утверждение. Из устойчивости по Ляпунову при  фиксированного (ненулевого) решения
фиксированного (ненулевого) решения 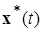 системы (1.2.1) не следует его ограниченность.
системы (1.2.1) не следует его ограниченность.
Верно и обратное: из ограниченности решения 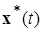 системы (1.2.1), вообще говоря, не следует его устойчивость по Ляпунову при
системы (1.2.1), вообще говоря, не следует его устойчивость по Ляпунову при  .■
.■
4. Для сокращения записи здесь и далее полезно использовать кванторы общности  и существования
и существования  , и тогда определение 1 можно записать так:
, и тогда определение 1 можно записать так:
Не нашли, что искали? Воспользуйтесь поиском: