Положение равновесия. Тривиальное решение.

Важным частным случаем фиксированного решения, исследуемого на устойчивость, является нулевое решение (тождественно равное нулю на ), или так называемое тривиальное решение. Дадим соответствующие определения.

Определение. Решение системы (1.2.1) называется состоянием (положением) равновесия (критической точкой, точкой покоя) системы (1.2.1) тогда и только тогда, когда

. (1.2.7)

Определение. Положениеравновесия называется тривиальным решением системы (1.2.1) тогда и только тогда, когда

В этом случае говорят, что система (1.2.1) допускает тривиальное решение.

В частности, для тривиального решения системы (1.2.1), если она его допускает, определения устойчивости и асимптотической устойчивости формулируются так:

Определение 1'. Тривиальное решение системы (1.2.1) устойчиво по Ляпунову при , если для любых существует такое, что все решения системы (1.2.1), удовлетворяющие неравенству

,

а) бесконечно продолжимы вправо;

б) удовлетворяют и неравенству

для всех .■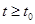

Определение 2'. Тривиальное решение системы (1.2.1) асимптотически устойчиво по Ляпунову при , если:

а) тривиальное решение устойчиво по Ляпунову при ;

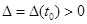б) для любого существует такое, что все решения , удовлетворяющие неравенству

,

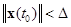обладают предельным свойством вида

.■

Определение 3 (равномерной устойчивости). Устойчивость по Ляпунову при называется устойчивостью, равномерной по (равномерной на 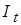), если в определении 1 выбор 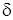- окрестности не зависит от выбора (зависит только от выбора ).■

Определение 4 (экспоненциальной устойчивости). Решение 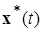системы (1.2.1) называется экспоненциально устойчивым по Ляпунову при , если найдутся и (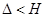) такие, что все решения 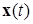, удовлетворяющие неравенству

удовлетворяют следующему неравенству:

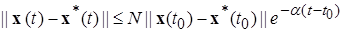, (1.2.8)

где 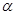, N – некоторые положительные числа, выбор которых в неравенстве (1.2.8) не зависит от выбора решений 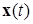, т.е. существуют такие 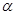, N, что все решения, исходящие из Δ-окрестности, удовлетворяют неравенству (1.2.8).■

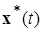Число называется степенью экспоненциальной устойчивости решения , окрестность называется областью экспоненциальной сходимости (экспоненциальной аттрактивности) этого решения.

Замечание. Очевидно, что определение 3 легко применить к экспоненциальной устойчивости, характеризуя ее равномерность по (равномерность на ).■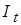

Пример. Можно доказать следующее утверждение: из экспоненциальной устойчивости решения x *(t) системы (1.2.1) следует его асимптотическая устойчивость по Ляпунову при t →+∞.

Доказательство. Доказательство проведем на так называемым языке ε, δ – окрестностей.

а) Докажем, что из экспоненциальной устойчивости следует устойчивость по Ляпунову для решения x *(t). Пусть x *(t) – экспоненциально устойчиво, т.е. такое, что имеет место неравенство (1.2.8). Для любого и любого фиксированного выберем

Тогда для любого решения х (t), удовлетворяющего неравенству ,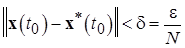

следует в силу неравенства (1.2.8), что

,

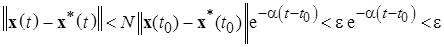так как .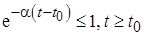

Следовательно, решение - устойчиво по Ляпунову при .

б) Очевидно, что все решения , удовлетворяющие (при некотором ) неравенству

,

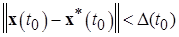обладают предельным свойством

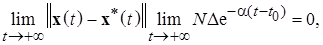
что также следует из неравенства (1.2.8), т.е. решение обладает свойством притяжения (аттрактивности).

Следовательно, решение - асимптотически устойчиво, что и требовалось доказать.□

Определение 5 (асимптотической устойчивости в целом). Пусть система (1.2.1) определена во всем , т.е. в определении области 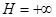. Решение называется асимптотически устойчивым в целом (или глобально асимптотически устойчивым), если его областью притяжения является все , т.е. ■

Замечание. Аналогично определяется экспоненциальная устойчивость в целом (глобальная экспоненциальная устойчивость). ■

Не нашли, что искали? Воспользуйтесь поиском: