Тема. Розв’язування задач на складання рівнянь ліній другого порядку:гіперболи, параболи

Мета роботи: навчитись складати рівняння кривих другого порядку за виглядом рівнянь ліній досліджувати їх особливості.

Наочне забезпечення та обладнання:

1. Інструкційні картки;

2. Приклади задач;

3. Роздаткові матеріали: опорні конспекти “Основні формули аналітичної геометрії”

4. Обчислювальні засоби.

Теоретичні відомості про гіперболу

Гіперболою називається геометричне місце точок модуль різниці відстаней для кожної з яких до двох даних фіксованих точок (фокусів) є величина стала, менша за відстань між фокусами і дорівнює . Найпростіше рівняння гіперболи:

,

де - дійсна піввісь гіперболи, - уявна піввісь.

Якщо - відстань між фокусами, то . При = гіпербола називається рівносторонньою, її рівняння має вигляд: Фокуси гіперболи знаходяться на її дійсній осі. Ексцентриситет гіперболи – це відношення фокусної відстані до довжини дійсної осі:

Асимптоти гіперболи – прямі, що задаються рівняннями .

Якщо фокуси гіперболи лежать на осі , то її рівняння має вигляд:

або ,

а рівняння асимптот такої гіперболи .

Рівняння рівносторонньої гіперболи з фокусами на осі має вигляд:

Гіперболи:

і

називаються спряженими.

В усіх задачах на гіперболу передбачено, що осі симетрії гіперболи співпадають з осями координат.

Задача №1. Скласти рівняння гіперболи, що має асимптотами прямі і проходить через точку (-5;2).

Задача №2. Скласти рівняння гіперболи, якщо її вершини лежать в точках і фокуси в точках .

Задача № 3. Дано рівняння гіперболи 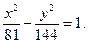Знайти координати її вершин і фокусів.

Не нашли, что искали? Воспользуйтесь поиском: