
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Высказывания и операции над ними
МАТЕМАТИЧЕСКАЯ ЛОГИКА
В ТАБЛИЦАХ И ПРИМЕРАХ
Екатеринбург, 2014
ОДОБРЕНО
Цикловой методической комиссией
«Естественнонаучных дисциплин»
Протокол №______
от «____» _____ 2014 г
Председатель ЦМК
_________ О.В. Алферьева
Автор: Алферьева О.В., преподаватель дисциплин математического цикла.
Рецензенты: Поликарпова С.В., преподаватель дисциплины «Архитектура аппаратных средств», Патракова Т.Д., преподаватель дисциплин математического цикла.
Содержание
Высказывания и операции над ними. 4
Формулы алгебры логики. 5
Булевы функции. 6
Логические законы.. 7
СДНФ и СКНФ.. 8
Карты Карно. МДНФ.. 9
Предикаты и кванторы.. 10
Понятие множества. 11
Операции над множествами. 12
Сравнение множеств. 13
Отношения на множествах. 14
Свойства отношений. 15
Список использованных источников. 17
Высказывания и операции над ними


| Название логической операции | Обозна-чение | Определение | Читается | Таблица истинности | |||||||||||||||
| Инверсия, логическое отрицание | P, 
| • Отрицанием высказывания Р называется высказывание 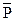 , которое истинно, когда высказывание Р ложно, и ложно, когда высказывание Р истинно. , которое истинно, когда высказывание Р ложно, и ложно, когда высказывание Р истинно.
| «НЕ Р» или «НЕВЕРНО, ЧТОР» |
| |||||||||||||||
| Конъюнкция, логическое умножение | &, ∙, 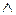
| • Конъюнкцией двух высказываний Р и Q называется составное высказывание Р 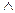 Q, которое принимает истинное значение только в том случае, когда истинны обе его составные части. Q, которое принимает истинное значение только в том случае, когда истинны обе его составные части.
| «Р И Q» |
| |||||||||||||||
| Дизъюнкция, логическое сложение | +, 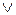
| • Дизъюнкцией двух высказываний Р и Q называется составное высказывание Р  Q, которое принимает истинное значение, если хотя бы одна из его составных частей имеет истинное значение. Q, которое принимает истинное значение, если хотя бы одна из его составных частей имеет истинное значение.
| «Р ИЛИQ» |
| |||||||||||||||
| Строгая дизъюнкция, сумма по модулю 2, исключающее или | 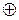 , , 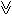
| • Строгой дизъюнкцией двух высказываний Р и Q называется составное высказывание Р  Q, которое принимает истинное значение, если только одна из его составных частей имеет истинное значение. Q, которое принимает истинное значение, если только одна из его составных частей имеет истинное значение.
| «ЛИБО Р, ЛИБО Q» |
| |||||||||||||||
| Импликация, следование | → | • Импликацией двух высказываний Р и Q называется составное высказывание Р→Q, которое принимает ложное значение, если высказывание Р истинно, а высказывание Q ложно. (Р→Q ложно, только если из истины следует ложь) | «ЕСЛИ Р, ТО Q», или «ИЗ Р СЛЕДУЕТ Q», или «Р ВЛЕЧЕТ Q» |
| |||||||||||||||
| Эквиваленция, равносильность |  , ~ , ~
| • Эквиваленцией двух высказываний Р и Q называется составное высказывание Р  Q, которое принимает истинное значение, тогда и только тогда, когда оба высказывания истинны, или оба высказывания ложны. Q, которое принимает истинное значение, тогда и только тогда, когда оба высказывания истинны, или оба высказывания ложны.
| «РТОГДА И ТОЛЬКО ТОГДА, КОГДА Q» или «РРАВНО-СИЛЬНО Q», |
Не нашли, что искали? Воспользуйтесь поиском:
|
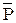
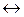 Q
Q