Виды бинарных отношений на множестве A

1) Обратное отношение для R: .

2) Дополнение R: .

3) Тождественное: .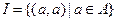

4) Универсальное: .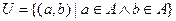

Композиция отношений

Пример. , , .

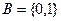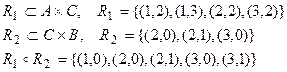
Пример. Пусть A ={0,1}, B ={К, Л, О}, , {(0,К),(0,Л),(1,К),(1,О)}. Найти ядро отношения , т.е. .

Найдем обратное отношение ={(К,0),(Л,0),(К,1),(О,1)}.

Затем найдем композицию отношения и обратного для него отношения :

= {(0,0),(0,1),(1,0),(1,1)}.

Свойства отношений

Пусть , т.е. - бинарное отношение на множестве A.

Читается: всякий элемент из множества А находится в отношении сам с собой.

Пример 1. Рассмотрим отношение , , 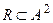A – множество студентов техникума, тогда условие 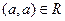означает, что любой студент техникума является одногруппником самого себя, что не верно, значит, отношение не является рефлексивным.

Пример 2. Рассмотрим отношение , , 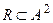A – множество всех действительных чисел, тогда условие 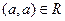означает, что любое действительное число больше либо равно самому себе (), что верно, значит, отношение является рефлексивным.

Читается: для всяких элементов из множества А, если элемент a находится в отношении c элементом b, то и элемент b находится в отношении c элементом a.

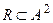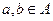
Пример 1. Рассмотрим отношение , , A – множество студентов техникума, тогда условие означает, что если студент техникума a является одногруппником студента b, то студент b является одногруппником студента a, что верно, значит, отношение является симметричным.

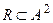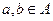
Пример 2. Рассмотрим отношение , , A – множество всех действительных чисел, тогда условие 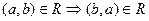означает, что если выполняется условие 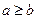, то выполняется и условие 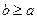, что не верно, значит, отношение не является симметричным.

Читается: для всяких элементов из множества А, отношение не может содержать пару одновременно с парой , если элемент a отличен от элемента b.

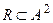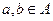
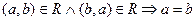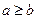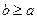Пример 1. Рассмотрим отношение , , A – множество всех действительных чисел, тогда условие тогда условие означает, что если выполняются условия и , то выполняется условие , что, верно, значит, отношение является антисимметричным.

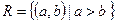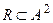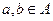
Пример 2. Рассмотрим отношение , , A – множество всех действительных чисел, тогда условие 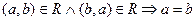означает, что если выполняются условия и , то выполняется условие , что не верно, значит, отношение не является антисимметричным.

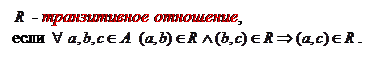
Читается: для всяких элементов из множества А, если элемент a находится в отношении c элементом b и элемент b находится в отношении c элементом с, то и элемент a находится в отношении c элементом с.

Пример 1. Рассмотрим отношение , , 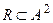A – множество студентов техникума, тогда условие 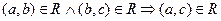означает, что если студент техникума a является одногруппником студента b и студент b является одногруппником студента с, то студент а является одногруппником студента с, что очевидно верно, значит, отношение является транзитивным.

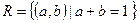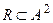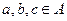
Пример 2. Рассмотрим отношение , , A – множество всех действительных чисел, тогда условие 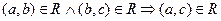означает, что если выполняются условия и , то выполняется и условие , что не верно (при , , 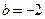, имеем и и ), значит, отношение не является транзитивным.

Читается: Если два элемента различны, то элемент a находится в отношении c элементом b или элемент b находится в отношении c элементом a.

Пример 1. Рассмотрим отношение , , A – множество студентов техникума, тогда условие 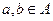означает, что для любых двух студентов техникума a и b, или студент a является одногруппником студента b или студент b является одногруппником студента a, что очевидно не верно, значит, отношение не является полным.

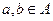
Пример 2. Рассмотрим отношение , , A – множество всех действительных чисел, тогда условие означает, что для любых двух различных чисел a и b либо выполняется условие 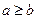, либо выполняется и условие 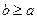, что, верно, значит, отношение является полным.

Список использованных источников

1. Галушкина Ю.И., Марьямов А.Н. Конспект лекций по дискретной математике. – М.: АЙРИС-ПРЕСС, 2008.

2. Дискретная математика: Учебник для студ. учреждений сред. проф. образования / М. С. Спирина, П. А. Спирин. – М.: Издательский центр «Академия», 2012.

3. Новиков Ф. А. Дискретная математика для программистов. – СПб.: Просвещение, 2001.

4. Хаггарти Р. Дискретная математика для программистов. – М.: Техносфера, 2003.

Не нашли, что искали? Воспользуйтесь поиском: