
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Пример.Построить таблицу истинности формулы .
| Порядок действий: | |||||

| 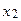
| 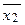
| 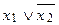
| 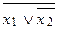
| 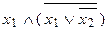
|
1. Определим порядок действий в формуле:  .
.
2. Пользуясь определениями логических операций 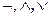 , заполним таблицу истинности.
, заполним таблицу истинности.






Булевы функции
 Булевы функции находят применение в проектировании и упрощении логических схем. Такие схемы встречаются в электронных устройствах, используемых в компьютерах, калькуляторах, телефонных системах и ряде других устройств.
Булевы функции находят применение в проектировании и упрощении логических схем. Такие схемы встречаются в электронных устройствах, используемых в компьютерах, калькуляторах, телефонных системах и ряде других устройств. 


Булевы функции часто задаются таблично. Эти таблицы напоминают таблицы истинности логических операций, поэтому сами булевы функции часто называют булевыми операциями, а соответствующие им таблицы таблицами истинности.
| Значения переменной | Булевы функции одной переменной | |||
| х | Название функции | Формула, реализующая функцию функции | ||
| y0 | Тождественный ноль |  0 0
| ||
| y1 | Тождественная переменной | 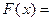 х х
| ||
| y2 | Отрицание переменной | 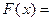 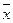
| ||
| y3 | Тождественная единица переменной | 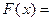 1 1
|
| Значения переменной | Булевы функции двух переменных | |||||
| х1 | Название функции | Формула, реализующая функцию | ||||
| х2 | ||||||
| y0 | Тождественный ноль |  0 0
| ||||
| y1 | Конъюнкция, И |  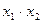
| ||||
| y2 | Отрицание импликации |  
| ||||
| y3 | Тождественная первой переменной |  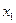
| ||||
| y4 | Отрицание импликации |  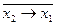
| ||||
| y5 | Тождественная второй переменной |  
| ||||
| y6 | Сумма по модулю два, строгая дизъюнкция |  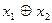
| ||||
| y7 | Дизъюнкция, ИЛИ |  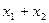
| ||||
| y8 | Стрелка Пирса, ИЛИ-НЕ |  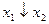
| ||||
| y9 | Эквиваленция |  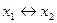
| ||||
| y10 | Инверсия второй переменной |  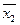
| ||||
| y11 | Импликация |  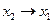
| ||||
| y12 | Инверсия первой переменной |  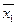
| ||||
| y13 | Импликация |  
| ||||
| y14 | Штрих Шеффера, И-НЕ |  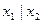
| ||||
| y15 | Тождественная единица |  1 1
|
Логические законы
| Название закона | Запись закона в алгебре высказываний | Запись закона в алгебре Буля |  Смысл Смысл
|
| Коммутативный | А 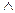 В = В В = В 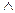 А
А А
А  В = В В = В  А А
| 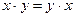

| Коммутативность означает, что можно менять местами члены конъюнкции (дизъюнкции). |
| Ассоциативный |  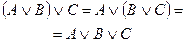
|  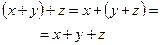
| Ассоциативность означает, что можно не ставить скобки при нескольких последовательных применениях конъюнкции (дизъюнкции) или наоборот ставить их, так как удобно. |
| Дистрибутивный | А 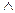 (В (В  С) = (А С) = (А 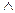 В) В)  (А (А 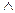 С)
А С)
А  (В (В 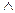 С) = (А С) = (А  В) В) 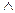 (А (А  С) С)
| 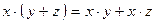
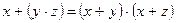
| Дистрибутивность означает, что можно раскрывать скобки при применениях конъюнкции к дизъюнкции и наоборот. |
| Идемпотентность | А 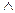 А = А
А А = А
А  А = А А = А
| 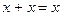
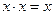
| Определяет результат конъюнкции (дизъюнкции) для двух одинаковых членов. |
| Закон исключенного третьего | 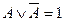
| 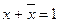
| Для каждого высказывания истинно либо оно, либо его отрицание. |
| Закон противоречия | 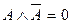
| 
| Одно и то же высказывание не может быть одновременно истинным и ложным. |
| Закон двойного отрицания | 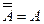
| 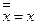
| Двойное отрицание высказывания равносильно этому высказыванию. |
| Законы действий с константами | 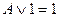 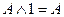
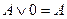 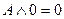
|  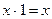
 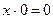
| Действия с 0 и 1. |
| Закон Де Моргана | 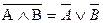
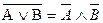
| 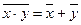

| Инверсию над конъюнкцией (дизъюнкцией) переменных можно «протащить» на каждую переменную, но знак 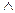 ( ( ) при этом меняем на ) при этом меняем на  ( (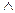 ). ).
|
| Закон поглощения | А 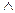 (А (А  В) = А
А В) = А
А  (А (А 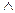 В) = А В) = А
| 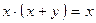
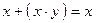
| Переменная у (В) «поглощается», остается только переменная х (А) |
| Снятие импликации, эквиваленции и строгой дизъюнкции | 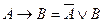 , ,
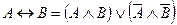 , ,
 . .
| 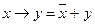 , ,
 , ,
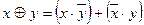 . .
| Закон позволяет перейти от операций
 к базовым операциям к базовым операциям 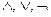 . .
|
СДНФ и СКНФ


|

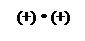



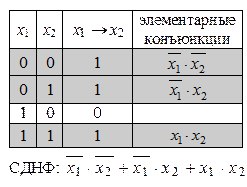 Алгоритм составления СДНФ:
Алгоритм составления СДНФ:
1. Составляем таблицу истинности формулы.
2. Выбираем наборы переменных, на которых функция равна 1.
3. Каждому выбранному набору ставим в соответствие полную совершенную элементарную конъюнкцию:
- если значение переменной в этом наборе равно 0, то эта переменная берется с отрицанием.
- если значение переменной в этом наборе равно 1, то эта переменная берется без отрицания.
4. Соединяем полученные элементарные конъюнкции операцией дизъюнкции (+), получаем СДНФ.
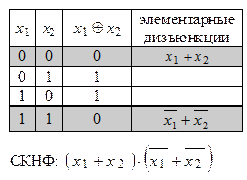 Алгоритм составления СКНФ:
Алгоритм составления СКНФ:
1. Составляем таблицу истинности формулы.
2. Выбираем наборы переменных, на которых функция равна 0.
3. Каждому выбранному набору ставим в соответствие полную совершенную элементарную дизъюнкцию:
- если значение переменной в этом наборе равно 1, то эта переменная берется с отрицанием.
- если значение переменной в этом наборе равно 0, то эта переменная берется без отрицания.
4. Соединяем полученные элементарные дизъюнкции операцией конъюнкции (•), получаем СКНФ.
Карты Карно. МДНФ
|




| 
| 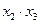
| 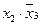
| |
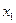
| ||||
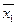
|
Пример. Минимизируем 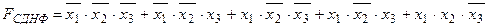 функции трех переменных с помощью карт Карно.
функции трех переменных с помощью карт Карно.
1. Разобьем переменные на две группы x1 и x2x3.
2. Заполняем карту Карно.
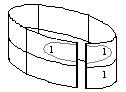 3. Объединяем соседние единицы контурами, считаем соседними ячейки расположенные на противоположных краях карты.
3. Объединяем соседние единицы контурами, считаем соседними ячейки расположенные на противоположных краях карты.
 
| 
| 
| 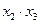
|  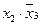
|
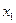
|  1 1
|  1 1
| ||
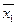
|  1 1
|
4. Внутри каждого контура исключаем члены, дополняющие друг друга до 1 (т.е. 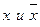 ).
).
5. Объединим оставшиеся члены дизъюнкцией.

 6. Запишем полученное выражение
6. Запишем полученное выражение 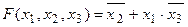 .
.
Предикаты и кванторы


Виды предикатов
 - одноместный предикат;
- одноместный предикат;
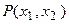 - двух местный предикат;
- двух местный предикат;
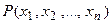 - n – местный предикат.
- n – местный предикат.
Пример.
Одноместный предикат 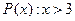 .
.
Двух местный предикат 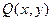 : Студент x учится в группе y.
: Студент x учится в группе y.
Не нашли, что искали? Воспользуйтесь поиском: