Чувствительность к форме сигнала

Сигнал на входе измерительной системы служит носителем информации о значении физической величины, которая должна быть измерена. Отклик системы на входной сигнал в общем случае зависит от формы (вида или структуры) этого входного сигнала.

Часто классификацию сигналов проводят по следующим признакам. Сиг­нал может быть константой, то есть не зависеть от времени (статический сиг­нал), например, постоянное напряжение или постоянный ток. Обычно сигнал изменяется, но только очень медленно; такой сигнал называют квазистатическим. Однако не менее часто сигнал является функцией времени (динамичес­кий сигнал). Если сигнал x(t) повторяется во времени каждые Т секунд, то он называется периодическим сигналом с периодом T (для всех t: x(t) = x(t + T); см. рис. 2.29(a)). Частота повторения равна f=1 / T. Отношение 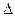t/ T для импуль­сных сигналов (см. рис. 2.29(b)), по определению, представляет собой коэффициент заполнения. Сигналы с очень малым коэффициентом заполнения (импульсы) измерять трудно, и часто они являются причиной сильных наводок на соседние измерительные устройства. Когда зависящий от времени сигнал не является периодическим, его называют одиночным сигналом (одиночной реали­зацией) или неустановившимся сигналом (переходным процессом). Примерами таких сигналов служат шумовые напряжения и переходные явления, такие как выбросы или звон (затухающие колебания) в системах с переключениями. Как правило, периодические сигналы легче измерять, чем непериодические. В час­тности, поэтому при исследовании переходной характеристики системы усло­вия ее воспроизведения повторяют многократно, получая, таким образом, более легкий для измерения периодический сигнал.

Динамический сигнал можно анализировать как во временной области, так и в частотной области. Наблюдение структуры колебания, например, с помощью осциллографа, осуществляется во временной области, тогда как частотное наполнение (свойства) изучают с помощью спектроанализатора в частотной области.

Следовательно, для однозначного определения того, что такое «чувстви­тельность измерительной системы» в случае динамического сигнала необхо­димо установить, на какую характеристику сигнала реагирует наша измери­тельная система. Другими словами: значение какого параметра сигнала изме­ряется? Применительно к динамическому измерительному сигналу x(t) мож­но указать следующие характерные значения:

- Пиковое значение х_р:

х_р =max\x(t).

- Полный размах х_рр:

х_рр = max {x(t)}-min {x(t)}.

Рис. 2.29. Периодические сигналы, (а) Сложный периодический сигнал обще­го вида. (b) Импульсный сигнал с коэффициентом заполнения 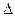Т/Т =1/T.

Целесообразно как можно реже использовать пиковое значение и полный размах, так как оба они очень чувствительны к возмущениям типа шума, накладывающегося на полезный сигнал. Большие ошибки в х и x возникают также из-за нелинейных искажений сигнала. Значительно менее чувстви­тельными к искажениям и помехам являются следующие параметры сигнала:

- Среднее по времени значение x_avg:

x_avg = .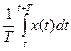

Среднее значение периодического сигнала находят на интервале време­ни, в который укладывается целое число периодов: Т = п /f, п — целое.

Среднее значение синусоидального сигнала равно нулю.

- Среднее значение от абсолютной величины |x|_avg:

|x|_avg = .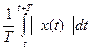

Когда говорят о среднем значении синусоидального сигнала, обычно имеют в виду среднее значение абсолютной величины синусоидального колебания.

- Действующее значение x :

x = .

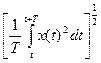Сейчас будет показано, что применение действующего значения в качестве характеристики измерительного сигнала полезно. Мгновенная мощность p(t), рассеиваемая на резисторе R приложенным к нему измерительным сигналом x(t), равна

p(t)= .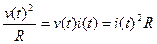

Здесь i(t) — ток, текущий по резистору R. Средняя мощность, рассеива­емая на резисторе за время T, равна

P _avg =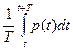

=

=

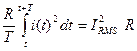
Следовательно, воспользовавшись действующими значениями напряже­ния и тока, мы легко можем найти (среднее) значение мощности, рассеи­ваемой измерительным сигналом. Очевидно, что можно также принять, по определению, что среднеквадратические значения напряжения и тока — это такие величины постоянного напряжения и постоянного тока, при ко­торых в резисторе переходит в тепло такое же количество энергии, какое рассеивается в нем при воздействии измеряемых напряжения или тока (теп­ловое определение действующего значения).

При построении измерительной системы решают вопрос о том, на какое характерное значение сигнала будет реагировать система. Измерительная сис­тема может воспроизводить мгновенные значения сигнала (осциллограф), от­кликаться на среднее значение (измеритель с подвижной катушкой), реаги­ровать на среднее значение от абсолютной величины (измеритель с подвиж­ной катушкой, снабженный выпрямителем/усилителем) или быть чувстви­тельной к среднеквадратическому значению (электродинамический вольтметр).

Для синусоидального сигнала x(t) = asin(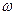 t), изображенного на рис. 2. 30, значения перечисленных параметров равны:

х = a; x 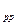=2a; |x|_avg = ; x = .

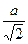Отношение x /|x|_avg называют коэффициентом формы сигнала x(t), а отно­шение х_р/x _RMS — коэффициентом амплитуды этого сигнала (его пик-фактором). Для синусоидального колебания коэффициент формы равен 1,11, а пик-фактор — . Коэффициент формы важен в том случае, когда измерительная система проградуирована в действующих значениях (для синусоидального колебания), а фактически ею измеряется среднее значение от абсолютной величины. Именно так обстоит дело во многих электронных вольтметрах. Пик-фактор важен при измерениях шумовых и импульсных сигналов. Часто бывает желательно знать действующее значение таких сигналов, однако при этом необходимо, чтобы пиковые значения сигналов оставались в линейном диапазоне системы; только в этом случае мы избежим ошибок измерения, обусловленных насыщением.

Не нашли, что искали? Воспользуйтесь поиском: