
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Разрешающая способность
Разрешающая способность (разрешение) измерительной системы — это размер шага, на который может быть настроена система, или шага, с которым на индикатор выводится результат действия системы. По определению, разрешающая способность — это наименьший интервал 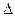 х значения измеряемой величины х, который все еще вызывает изменение результата измерения у. Численно разрешающая способность R выражается в виде:
х значения измеряемой величины х, который все еще вызывает изменение результата измерения у. Численно разрешающая способность R выражается в виде:

Рис. 2.30. Полный размах хрр, действующее значение x  и среднее значение от абсолютной величины |x|avg сигнала синусоидальной формы.
и среднее значение от абсолютной величины |x|avg сигнала синусоидальной формы.
R=  .
.
Иногда речь идет о максимальном значении разрешения. Оно достигается при максимальной величине х, которая может быть измерена с помощью этой системы без насыщения, искажений и перегрузки:
 .
.
Разрешающая способность R имеет конечное значение для всех систем, в которых результат измерения не увеличивается непрерывно с ростом измеряемой величины х. Примером таких систем являются механическая измерительная система с люфтом и трением покоя, проволочный потенциометр, ступенчатый аттенюатор и цифровой индикатор; во всех этих случаях выходная величина у не растет непрерывно с увеличением входного воздействия, а меняется малыми скачками 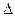 у.
у.
Если разрешение системы конечно, то результат измерений оказывается квантованным; при этом возникает ошибка квантования. Ошибки, являющиеся следствием квантованности результата измерения, можно разделить на ошибки усечения и ошибки округления. Ошибка усечения происходит в том случае, когда в системе не принимаются во внимание десятичные знаки справа от младшего указываемого десятичного разряда: остаток просто опускают. Обычно это имеет место в алфавитно-цифровых индикаторах, например, в цифровом вольтметре. Величина допускаемой при этом ошибки равна 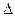 х/х, то есть отношению наименьшего возможного шага
х/х, то есть отношению наименьшего возможного шага 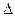 х к воспроизводимой на индикаторе величине х. Ошибка округления происходит в том случае, когда в наименьшем указываемом десятичном разряде учитывается остаток путем округления до ближайшего значения в этом разряде. При этом ошибка равна
х к воспроизводимой на индикаторе величине х. Ошибка округления происходит в том случае, когда в наименьшем указываемом десятичном разряде учитывается остаток путем округления до ближайшего значения в этом разряде. При этом ошибка равна 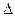 х / 2х, то есть половине наименьшего шага, деленной на индицируемое значение. Если при проведении нуль-измерения мы применим эталон, который можно подстраивать только в ступенчатом режиме, и будем изменять задаваемую эталоном величину до тех пор, пока нуль-орган не покажет наименьший отсчет, то будет иметь место ошибка округления.
х / 2х, то есть половине наименьшего шага, деленной на индицируемое значение. Если при проведении нуль-измерения мы применим эталон, который можно подстраивать только в ступенчатом режиме, и будем изменять задаваемую эталоном величину до тех пор, пока нуль-орган не покажет наименьший отсчет, то будет иметь место ошибка округления.
Нелинейность
В измерительной системе с независящей от частоты чувствительностью соотношение между выходным сигналом у и входным сигналом х линейно, когда функция у =f(x) представляет собой прямую линию; такие системы с частотно-независимой чувствительностью, у которых f( х) = ах + b, называют статическими системами. Для линейной частотно-зависимой системы соотношение между y(t) и x(t) задается линейным дифференциальным уравнением. Это такое уравнение, в котором содержатся только члены первого порядка в отношении у и производных от у. Системы с частотно-зависимой чувствительностью называют динамическими системами. Если на вход линейной измерительной системы подать сумму двух синусоидальных сигналов
х 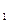 = а
= а 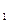 sin (
sin (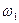 t +
t + 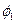 ) и х
) и х  = а
= а  sin (
sin ( t +
t +  ), то выходной сигнал также будет состоять из двух синусоидальных сигналов у
), то выходной сигнал также будет состоять из двух синусоидальных сигналов у 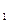 = b
= b 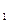 sin(
sin(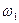 t +
t +  ) и у
) и у  = b
= b  sin (
sin ( t +
t +  ) с теми же самыми частотами, что и во входном сигнале (изохронизм), но уже с другими мплитудами и фазами.
) с теми же самыми частотами, что и во входном сигнале (изохронизм), но уже с другими мплитудами и фазами.
Для линейных систем справедлив принцип суперпозиции) это означает, что в случае, когда входной сигнал х 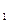 порождает на выходе сигнал у
порождает на выходе сигнал у 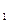 а входной сигнал х
а входной сигнал х  вызывает появление на выходе сигнала у
вызывает появление на выходе сигнала у  линейная комбинация а х
линейная комбинация а х 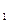 + b2 х
+ b2 х  на входе приведет к возникновению на выходе сигнала а у
на входе приведет к возникновению на выходе сигнала а у 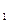 + b у
+ b у  . Принцип суперпозиции применим только к тем составляющим сигнала на входе системы, которые обусловлены входными воздействиями; возможные ошибки смещения здесь не принимаются во внимание.
. Принцип суперпозиции применим только к тем составляющим сигнала на входе системы, которые обусловлены входными воздействиями; возможные ошибки смещения здесь не принимаются во внимание.
Если сумма двух синусоидальных колебаний разных частот подана на вход нелинейной системы, то выходной сигнал будет содержать гармоники. Гармониками являются синусоидальные колебания с частотами n w 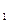 , и k w 2 соответственно, где n и к — целые числа. При п, к = 1 мы имеем дело с основными гармониками, а большим значениям пик соответствуют высшие гармоники n -го и k -го порядков. Кроме того, в выходном сигнале появятся также составляющие с суммарными и разностными частотами п
, и k w 2 соответственно, где n и к — целые числа. При п, к = 1 мы имеем дело с основными гармониками, а большим значениям пик соответствуют высшие гармоники n -го и k -го порядков. Кроме того, в выходном сигнале появятся также составляющие с суммарными и разностными частотами п 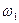 ± к
± к  , где
, где 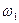
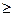
 и п
и п 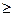 к. Помимо этого выходной сигнал может иметь также постоянную составляющую.
к. Помимо этого выходной сигнал может иметь также постоянную составляющую.
Раскладывая соотношение у =f(x) для статической нелинейной системы в ряд Тейлора, например, в точке х = 0, легко видеть, что
y=f(0)+xf’(0)+  f”(0)+….
f”(0)+….
Полагая
f(0)=0, f’(0)=c 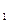 , f”(0)=c
, f”(0)=c  .
.
и т. д.
и
x(t)= х 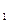 (t)+ х
(t)+ х  (t),
(t),
где х 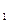 = а
= а 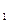 sin
sin 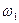 t
t
и х  = а
= а  sin
sin  t,
t,
получим:
y(t)=  (а
(а  + а
+ а  ) + с
) + с 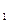 (а
(а 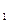 sin
sin 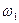 t+ а
t+ а  sin
sin  t)
t)
-  (а
(а  cos2
cos2 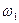 t+ а
t+ а  cos2
cos2  t)-
t)-  { а
{ а 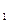 а
а  cos(
cos(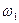 +
+  )t
)t
- а 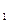 а
а  cos(
cos(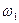 -
-  )t}+…
)t}+…
Степень нелинейности измерительной системы характеризуется нелинейными или гармоническими искажениями. Искажение такого рода измеряется путем подачи на вход измерительной системы одиночного синусоидального колебания. Коэффициент искажения, по определению, равен отношению действующего значения уп п-й гармоники к действующему значению у 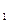 основной (первой) гармоники. Таким образом, коэффициент искажения, обусловленного п-й гармоникой, определяется как
основной (первой) гармоники. Таким образом, коэффициент искажения, обусловленного п-й гармоникой, определяется как
 (n>1).
(n>1).
Полный коэффициент искажений, обусловленных п — 1 гармониками (за исключением основной гармоники (п = 1)), равен
 .
.
Это соотношение легко понять, приняв во внимание, что корень из суммы квадратов действующих значений гармоник представляет собой действующее значение всех п — 1 гармоник:
 .
.
Степень статической (частотно-независимой) нелинейности часто определяют по-другому. Предположим, что в действительности соотношение между у и х задается функцией у = f(x), как показано на рис. 2.31. Лучшим линейным приближением кривой у = f(x), является прямая у = ах. В этом случае мерой нелинейности измерительной системы может служить максимальное значение выражения

в пределах всего динамического диапазона измерительной системы. Об определенной таким образом нелинейности говорят также, как о нелинейности с нулевым смещением.
Никакая измерительная система не является идеально линейной; она всегда линейна лишь приближенно (например, в малом интервале значений входного сигнала х). Сейчас мы кратко рассмотрим несколько видов нелинейности, которые могут иметь место в практических измерительных системах. Прежде всего речь пойдет о некоторых видах статической нелинейности.
- Насыщение и ограничение. Нелинейность такого рода характеризуется уменьшением дифференциальной чувствительности S 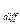 с ростом входного сигнала х. Как показано на рис. 2.32, в случае ограничения такое ослабление наступает резко, а в случае насыщения — постепенно. Чтобы предотвратить выход измерительной системы из строя, когда она оказывается перегружен ной слишком большим входным сигналом,
с ростом входного сигнала х. Как показано на рис. 2.32, в случае ограничения такое ослабление наступает резко, а в случае насыщения — постепенно. Чтобы предотвратить выход измерительной системы из строя, когда она оказывается перегружен ной слишком большим входным сигналом,

Рис. 2.31. Статическая нелинейность.

Рис. 2.32. Примеры насыщения и ограничения в измерительной системе, (а) Нелинейные передаточные характеристики. (b) Сигнал y(t), возникающий на выходе системы под действием синусоидального входного сигнала x(t).
часто намеренно ограничивают размах выходного сигнала безопасными значениями.
— Гистерезис. Такая нелинейность вызывается различными кривыми на плоскости ху, выражающими связь между у и х при увеличении х и при уменьшении х (см. рис. 2.33). К гистерезису может привести, например, люфт в механической зубчатой передаче. Другой пример гистерезиса — это зависимость магнитной индукции В от напряженности поля Н у ферромагнитного материала (кривая намагничивания).
— Мертвая зона. Этот вид нелинейности обычно возникает в том случае, когда существуют одна или большее число областей, в пределах которых величина выходного сигнала у не зависит от входного сигнала х (см. рис. 2.34). Такая нелинейность может быть вызвана трением покоя. Объект (например, стрелка) не будет двигаться до тех пор, пока действующая сила не превысит трения покоя.
Помимо рассмотренных видов нелинейности, может встретиться также какая-либо их комбинация. Кроме того, существуют динамические (частотно-зависимые) виды нелинейности. Проявлением такой нелинейности являются эффекты, связанные с существованием максимальной скорости нарастания напряжения; этот пример мы проиллюстрируем с помощью осциллограмм. Если максимальный ток, который может отдавать усилитель сигнала, подаваемого на отклоняющие пластины осциллографа,

Рис. 2.33. (а) Гистерезис и (b) результирующий выходной сигнал y(t), являющийся откликом на синусоидальный сигнал x(t) на входе.
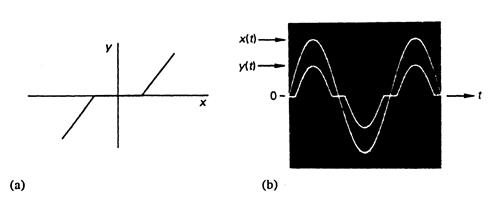
Рис. 2.34. (а) Мертвая зона в передаточной характеристике, системы. (b) Выходной отклик y(t) на синусоидальный входной сигнал x (t).
равен I  , а емкость отклоняющих пластин равна С, то время нарастания или спада на осциллограмме не может быть меньше определенной минимальной величины. Это значение определяется максимальной скоростью
, а емкость отклоняющих пластин равна С, то время нарастания или спада на осциллограмме не может быть меньше определенной минимальной величины. Это значение определяется максимальной скоростью
.
с которой может изменяться напряжение V  между пластинами, которому пропорционально отклонение луча. Таким образом, скорость перемещения луча по экрану пропорциональна производной от V
между пластинами, которому пропорционально отклонение луча. Таким образом, скорость перемещения луча по экрану пропорциональна производной от V  по времени. Как только частота или амплитуда входного сигнала становятся настолько большими, что максимальное значение d V
по времени. Как только частота или амплитуда входного сигнала становятся настолько большими, что максимальное значение d V  / dt оказывается превышенным, изображение искажается и колебание приобретает треугольную форму, как показано на рис. 2.35.
/ dt оказывается превышенным, изображение искажается и колебание приобретает треугольную форму, как показано на рис. 2.35.

Рис. 2.35. Искажения вследствие существования максимальной скорости нарастания: x(t)- входной сигнал, y(t)- выходной сигнал.
Не нашли, что искали? Воспользуйтесь поиском: