Пределы измерений, динамический диапазон

Пределы измерения определяются интервалом (x_min, x_max), внутри которого с помощью данной системы можно измерить нужную величину с требуемой точностью. Динамический диапазон измерительной системы равен отноше­нию х_maх I x_min. Величина х_тах обычно определяется предельным значением допустимой нелинейности, которая проявляется при больших входных сиг­налах. Величина x_min, как правило, определяется ошибками из-за смещения нуля и шумом, который становится тем более значительным, чем меньше сигнал. x_min — это наименьшее значение х, для которого может быть обеспечена заданная точность.

Возьмем, например, случай, когда надо с погрешностью ±3% измерить ток с помощью стрелочного прибора, собственная погрешность которого ±1% от всей шкалы. Динамический диапазон в этом случае равен лишь 3. Другой пример: с помощью измерительного усилителя нужно измерить на­пряжение с погрешностью 1%. Смещение нуля, отнесенное ко входу усили­теля, меньше 10 мкВ. Из-за нелинейности входное напряжение не должно превосходить 10 В, чтобы погрешность не превышала 1%. В этом примере динамический диапазон равен 10³.

Отклик системы

Реакция измерительной системы на приложенное ко входу воздействие на­зывается откликом системы. Отклик измерительной системы должен давать верное представление о воздействии; цель собственно измерения, очевид­но, состоит не столько в том, чтобы определять характеристики самой из­мерительной системы. Когда значения измеряемых физических величин меняются со временем (то есть в случае, когда измеряются динамические величины), важно точно знать, как измерительная система будет отслеживать эти изменения: поведение системы в динамике должно обеспечивать верное воспроизведение измеряемой величины.

Динамические свойства линейной измерительной системы целиком опре­деляются ее откликом на единичный скачок на входе (ее переходной харак­теристикой). Зная переходную характеристику можно найти время установ­ления или время считывания измерительной системы. На рис. 2.36 показаны сигнал x(t) на входе, имеющий вид скачка, и отклик y(t) измерительной системы. Здесь отклик нормирован по отношению к чувствительности по постоянному току 5(0), так что в пределе при t значения входного и выходного сигналов совпадают. Время установления отсчитывается от момента, когда происходит скачок на входе, до такой точки на оси времени, вслед за которой выходной сигнал y’(t), попав в заданный интервал (у_о — 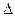у_о, у_о + 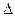у) допустимых отклонений от конечного значения у_о, остается в этом интервале. Отношение ± 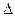у_о / у_о представляет собой относительную по­грешность измерительной системы. Время установления служит мерой быс­тродействия измерительной системы.

Динамическое поведение линейной измерительной системы также цели­ком определено, если известно, как она реагирует на синусоидальное коле­бание меняющейся частоты; то есть в том случае, когда мы знаем частот­ную характеристику.

Определение частотной характеристики измерительной системы приво­дит нас к (комплексной) зависимости чувствительности от частоты 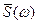. Чувствительность системы 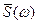состоит из двух характеристик: из ампли­тудно-частотной характеристики | 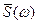| и фазо-частотной характеристики Arg 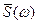. Этими двумя зависимостями динамическое поведение линейной системы определяется полностью. Характеристикой частотных свойств слу­жит ширина полосы 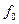. Значение 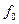представляет собой частоту, на которой мощность выходного сигнала падает вдвое по сравнению с максимальной мощностью на выходе. Следовательно, на частоте 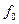амплитуда выходного сигнала уменьшается в раз по сравнению с ее значением на низких частотах. Поэтому значение амплитудно-частотной характеристики на час­тоте 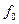равно S(0) / при условии, что на постоянном токе соответствую­щая величина равна S(0). Графики, приведенные на рис. 2.37, служат иллю­страцией сказанного. Так как 201og_I0(l/ ) 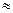-3, частоту называют также частотой спада на 3 дБ (сокращенно: точкой «-3 дБ»). Белы и децибелы служат логарифмической мерой отношения мощностей. Эта мера рассмот­рена в приложении A3.

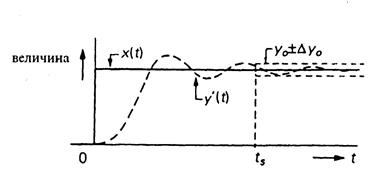
Рис. 2.36. Отклик y'(t) линейной измерительной системы на входное воздей­ствие x(t) в форме скачка. Переходная характеристика нормализована таким образом, что y'(t) = y(t) / S(0), где S(0) — чувствительность системы по постоянному току. Время установления прибора при допустимой погрешности ±Dy_o / у_о равно t .

Рис. 2.37. Частотная характеристика (f), состоящая из двух зависимос­тей: амплитудно-частотной характеристики | (f)| и фазо-частотной ха­рактеристики Arg (f). Ширина полосы системы равна f ₀.

Соотношение между входной величиной x (t) и выходной величиной y(f), а значит, и динамическое поведение линейной динамической системы мож­но представить в виде линейного дифференциального уравнения.

Если у зависит от х, то дифференциальное уравнение, описывающее соотношение между у и х, содержит не только функции от у и от х, но также и производные по времени от этих функций. В линейном дифферен­циальном уравнении имеются только такие члены, в которые функция у и ее производные входят в первой степени. Порядок дифференциального урав­нения равен наивысшему из порядков входящих в него производных.

У многих измерительных систем, различных по своей природе (электри­ческих, тепловых, акустических и т. д.), динамическое поведение оказыва­ется сходным. Если описывать эти системы в обобщенном виде в терминах V- и I -величин, то мы будем получать одни и те же дифференциальные уравнения. Следовательно, при изучении динамических систем можно огра­ничиться только дифференциальными уравнениями определенного вида. С точки зрения динамического поведения особенно важным является поря­док дифференциального уравнения. С учетом этого говорят об (измеритель­ной) системе п-го порядка и об отклике n -го порядка, если поведение систе­мы можно описать с помощью дифференциального уравнения n -го порядка. На практике большинство измерительных систем можно с достаточной точ­ностью описать линейным дифференциальным уравнением второго или бо­лее низкого порядка. Поэтому наше рассмотрение будет включать только случаи, когда п принимает одно из трех значений:

0, 1 или 2.

Не нашли, что искали? Воспользуйтесь поиском: