
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Системы нулевого порядка
Дифференциальное уравнение, описывающее систему нулевого порядка, является лишь простым алгебраическим уравнением. Система является статической или, говоря другими словами, частотно-независимой. Примером системы нулевого порядка служит потенциометрический преобразователь смещения, изображенный на рис. 2.38(a). В этом датчике смещение х преобразуется в пропорциональное ему выходное напряжение V. Предположим, что сопротивление между нижним концом потенциометра и движком равно R0 при х = 0, а максимальное сопротивление при х = х mах равно Rmax; тогда связь между выходным напряжением V и смещением х можно представить в виде
 .
.
Это частный случай уравнения вида:
у = ах + b.
Здесь b либо имеет нулевое значение, либо играет роль начального смещения, а a — чувствительность. Время установления ts равно нулю, а ширина полосы f0 равна бесконечности. В действительности, конечно, на очень высоких частотах чувствительность уменьшается, и у этого много причин (упругость, масса, паразитная емкость и т. д.); поэтому часто говорят, что такие системы являются системами квази-нулевого порядка. Это означает, что реакция таких систем является мгновенной в том диапазоне частот, который существенен при измерении данной величины. Систему, изображенную на рис. 2.38(b), также можно считать системой нулевого порядка. Выходное напряжение датчика Холла VH пропорционально току I  протекающему по пластине Холла и индукции В магнитного поля, образуемого центральным проводником. Кроме того, будет иметь место начальное смещение Vo. В разделе 3.2.3 будет показано, что
протекающему по пластине Холла и индукции В магнитного поля, образуемого центральным проводником. Кроме того, будет иметь место начальное смещение Vo. В разделе 3.2.3 будет показано, что
VH =  .
.

Рис. 2.38. Системы нулевого порядка: (а) потенциометрический преобразователь смещения и (b) датчик тока.
Здесь RH — постоянная Холла для данной пластины, а t — ее толщина. Поскольку значение В пропорционально току, текущему по центральному проводнику, такой датчик исключительно удобен для измерения больших токов. Он позволяет осуществить такое измерение, не разрывая проводник для подключения пробника, который внес бы дополнительное сопротивление.
У линейных систем первого порядка соотношение между входным сигналом x(t) и выходным сигналом y(t) выражается линейным дифференциальным уравнением первого порядка. Простой пример такой системы — ртутный термометр. Изменение длины столбика ртути, определяемое по откалиброванной шкале, служит выходным сигналом, а входным сигналом является измеряемая температура окружающей среды T  . Мы будем предполагать, что изменение длины столбика ртути прямо пропорционально изменению температуры ртути в резервуаре термометра. Поэтому для описания динамического поведения термометра вполне можно принять температуру Т
. Мы будем предполагать, что изменение длины столбика ртути прямо пропорционально изменению температуры ртути в резервуаре термометра. Поэтому для описания динамического поведения термометра вполне можно принять температуру Т 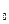 ртути в резервуаре за выходную величину (см. рис. 2.39(a)). Теплообмен между ртутью в резервуаре и окружающим воздухом должен происходить через стеклянную стенку с тепловым сопротивлением R. Тепловую емкость (теплоемкость) ртути в резервуаре обозначим С. Для малого приращения тепла
ртути в резервуаре за выходную величину (см. рис. 2.39(a)). Теплообмен между ртутью в резервуаре и окружающим воздухом должен происходить через стеклянную стенку с тепловым сопротивлением R. Тепловую емкость (теплоемкость) ртути в резервуаре обозначим С. Для малого приращения тепла 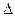 Q получим:
Q получим:
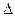 q = c
q = c 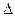 t
t 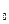 .
.
Кроме того,
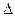 Q = I
Q = I 
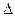 t =
t = 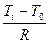
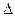 t,
t,
поэтому
rc  +t
+t 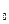 = t
= t  .
.
Другой пример системы первого порядка — это RС-цепь, приведенная на рис. 2.39(b). Пусть  и
и  - входное и выходное напряжения. С учетом того, что
- входное и выходное напряжения. С учетом того, что
 + IR=
+ IR= 
и
 ,
,

Рис.2.39. Два примера систем первого порядка: (а) ртутный термометр и (b) RС-цепь.
находим:
rc  +V
+V 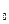 = V
= V  .
.
Полагая в обоих случаях RC = 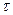 , мы можем представить эти линейные дифференциальные уравнения первого порядка в следующем общем виде:
, мы можем представить эти линейные дифференциальные уравнения первого порядка в следующем общем виде:
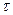
 + у = х.
+ у = х.
где х = x(t), а у = y(t). Таким образом, мы можем придти к выводу, что ртутный термометр и RC-цепь эквивалентны с точки зрения их динамического поведения.
Это дифференциальное уравнение решается просто. При скачкообразном входном сигнале
x(t) = 
при t 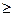 0
0
и
x(t)=0
при t <0,
а выходной сигнал y(t), или переходную характеристику, находим из
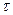
 + у = х.
+ у = х.
В операторной форме уравнение имеет вид:
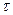 р + 1 = 0,
р + 1 = 0,
откуда
р = -  .
.
Общее решение таково: у = Сe  .
.
Частным решением при t  является функция y(t) = у
является функция y(t) = у 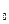 (конечное или установившееся значение):
(конечное или установившееся значение):
у = Сe  + у
+ у 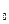 .
.
Полагая, что y(t) = 0 при / = 0, найдем:
y(t) = у 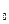 (1- e
(1- e  ).
).
Таким образом, переходная характеристика измерительной системы первого порядка имеет вид
y = у 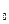 (1- e
(1- e  ),
),
где у 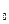 - конечное или установившееся значение, а
- конечное или установившееся значение, а 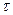 = RC - постоянная времени. Эта переходная характеристика изображена на рис. 2.40.
= RC - постоянная времени. Эта переходная характеристика изображена на рис. 2.40.
Если относительная погрешность измерительной системы не может превосходить  =
= 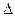 у
у 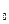 / у
/ у 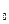 , то время установления ts равно
, то время установления ts равно

Это легко получить из выражения для переходной характеристики с помощью графика на рис. 2.40. Когда требуется очень малая относительная ошибка 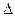 у
у 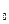 / у
/ у 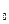 в конечном отсчете на выходе такой системы первого порядка, ее время установления ts становится чрезмерно большим. В примере с термометром на рис. 2.39(a) столбик ртути все медленнее ползет вверх к конечной отметке, которая достигается только при наступлении теплового равновесия между системой и ее окружением. Это является нежелательным свойством отклика первого порядка, когда речь идет о точных измерениях; время установления будет слишком большим.
в конечном отсчете на выходе такой системы первого порядка, ее время установления ts становится чрезмерно большим. В примере с термометром на рис. 2.39(a) столбик ртути все медленнее ползет вверх к конечной отметке, которая достигается только при наступлении теплового равновесия между системой и ее окружением. Это является нежелательным свойством отклика первого порядка, когда речь идет о точных измерениях; время установления будет слишком большим.
Частотная характеристика — это, по существу, отклик системы на синусоидальный входной сигнал x(t) = 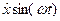 в установившемся режиме, то есть отклик, спустя длительное время после включения сигнала и подачи его на вход, когда все переходные явления затухнут. Частотную характеристику находят как частное решение дифференциального уравнения, описывающего систему первого порядка, при t
в установившемся режиме, то есть отклик, спустя длительное время после включения сигнала и подачи его на вход, когда все переходные явления затухнут. Частотную характеристику находят как частное решение дифференциального уравнения, описывающего систему первого порядка, при t  .
.
Частотную характеристику легко получить, применяя комплексные переменные в электрическом аналоге системы первого порядка, приведенном на рис. 2.39(b). Это дает:

(при 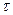 = RC).
= RC).

Рис. 2.40. Переходная характеристика системы первого порядка.
Модуль 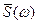 равен
равен
| 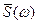 |=
|=  ,
,
а аргумент 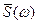 имеет вид:
имеет вид:
Arg 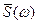 = -arctg
= -arctg 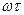 .
.
Амплитудно-частотная характеристика | 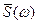 | и фазо-частотная характеристика Arg
| и фазо-частотная характеристика Arg 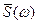 системы первого порядка представлены на рис. 2.41.
системы первого порядка представлены на рис. 2.41.
Ширина полосы f0 системы первого порядка определяется из равенства 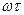 =1, так что fQ = 1 / 2
=1, так что fQ = 1 / 2  . На этой частоте сдвиг по фазе уже достигает значения -
. На этой частоте сдвиг по фазе уже достигает значения -  / 4 или -45°. На более высоких частотах сдвиг по фазе стремится к -90°', тогда как амплитуда выходного сигнала уменьшается почти до нуля.
/ 4 или -45°. На более высоких частотах сдвиг по фазе стремится к -90°', тогда как амплитуда выходного сигнала уменьшается почти до нуля.

Рис.
2.41. Частотная характеристика системы первого порядка.
Не нашли, что искали? Воспользуйтесь поиском: