ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ 1 ПО МЕХАНИКЕ

ВАРИАНТ 1

1. Зависимость координаты материальной точки от времени выражается уравнением: (м). Вычислите:

1) зависимость скорости и ускорения от времени;

2) максимальную скорость движения точки, её перемещение через 2 с, а также скорость и ускорение в момент времени t ₁ = 1 с;

3) постройте графики зависимости , и для моментов времени .

2. Вычислите ускорение грузов и силу натяжения нити. Нить нерастяжима, блок невесомый (рисунок 2.1), , коэффициент трения первого тела о поверхность .

3. Шар массой 0,5 кг движется с линейной скоростью 4 м/с по горизонтальной плоскости, а потом вкатывается вверх по наклонной плоскости. Вычислите высоту, на которую он вкатится. Мгновенная ось, относительно которой шар вращается в данный момент времени, есть точка соприкосновения шара с плоскостью.

4. Пластмассовый шар массой лежит на подставке с отверстием. Снизу в шар через отверстие попадает вертикально летящая пуля массы и пробивает его насквозь. При этом шар подскакивает на высоту . На какую высоту над подставкой поднимется пробившая шар пуля, если перед попаданием в шар она имела скорость ?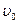

ВАРИАНТ 2

1. Тело движется так, что зависимость координаты от времени определяется уравнением: (м). Вычислите:

1) зависимость скорости и ускорения от времени;

2) среднюю скорость за вторую секунду;

3) путь, пройденный за 5 с и за пятую секунду;

4) начертите графики зависимости: , , ;

5) назовите характер движения тела.

2. Вычислите ускорения грузов и силу натяжения нити (рисунок 2.2). Нить нерастяжимая, невесомая, блок невесомый, кг, = 2 кг коэффициент трения первого тела о поверхность , внешняя сила =10 Н

3. К ободу однородного диска радиусом 0,2 см приложена постоянно касательная сила 100 Н. При вращении на диск действует сила трения, момент которой 5 Н ּ м. Вычислите массу диска, если известно, что он вращается с постоянным угловым ускорением 100 рад/с², а также кинетическую энергию в начальный момент времени.

4. Четыре одинаковых шара массы 20 г каждый расположены на одной прямой, на некотором расстоянии друг от друга. С крайним слева шаром соударяется шар такой же массы и размера, имеющий скорость 10 м/с и движущийся вдоль прямой на которой расположены шары. Найти кинетическую энергию системы после соударений, считая их абсолютно неупругими.

ВАРИАНТ 3

1. Зависимость координаты материальной точки от времени выражается уравнением: , м. Вычислите:

1) зависимость скорости и ускорения от времени;

2) скорость и ускорение в момент времени t = 1 c;

3) максимальную скорость точки;

4) перемещение через 3 с от начала движения;

5) постройте графики зависимостей: , , ;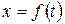

6) назовите характер движения тела.

2. Вычислите ускорения грузов и силу натяжения нити (рисунок 2. 3) Нить нерастяжимая, невесомая, блок невесомый, = 1 кг, = 2 кг, коэффициент трения первого тела о поверхность , внешняя сила F = 10 H, угол .

3. С наклонной плоскости, составляющий с горизонтом угол 30°, скатывается шар. Длина плоскости 4 м. Пренебрегая трением, вычислите линейное ускорение центра массы шара, время скатывания, скорость тела в конце наклонной плоскости.

4. На горизонтальной плоскости стоят два связанных нитью одинаковых бруска, между которыми расположена сжатая пружина, не скрепленная с брусками. Нить пережигают и бруски расталкиваются в разные стороны, скользят и останавливаются так, что расстояние между ними возрастает на величину . Найти потенциальную энергию сжатой пружины, если масса каждого бруска равна . Коэффициент трения между брусками и плоскостью равен .

ВАРИАНТ 4

1. Материальная точка движется в поле Земли согласно уравнениям движения 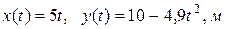. Вычислите:

1) зависимость проекций скорости ускорения на оси от времени;

2) время движения точки;

3) запишите уравнение траектории и определите характер движения точки;

4) начертите график зависимости ;

5) полное ускорение, начальную и конечную скорости движения, а также модуль перемещения.

2. Вычислите ускорения тел и силу натяжения нити (рисунок 2.4) Нить невесомая, нерастяжимая, блок невесомый, = 1 кг, = 2 кг, коэффициент трения первого тела о поверхность 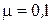, внешняя сила F = 10 H.

3. Сплошной цилиндр массой 1 кг и радиусом 0,05 м вращается вокруг оси, проходящей через его центр. В точке, наиболее удаленной от оси вращения, на цилиндр действует сила, касательная к поверхности. Угол поворота цилиндра меняется по закону . Вычислите величину силы, тормозящий момент силы, время равнозамедленного движения и кинетическую энергию в начале движения.

4. Клин высотой массы находится на идеально гладкой горизонтальной плоскости. На клине лежит брусок массы , который скользит без трения по клину. В начальный момент система покоилась, брусок находился на самом верху клина. Найти скорость клина в тот момент, когда брусок соскользнет с клина на плоскость. Наклонная плоскость клина имеет плавный переход к горизонтальной плоскости.

ВАРИАНТ 5

1. Движение тела в поле Земли определяется уравнениями . Вычислите:

1) зависимость проекций скорости и ускорения на оси от времени;

2) начальную и конечную скорости движения точки;

3) запишите уравнение траектории движения тела , постройте график зависимости для моментов времени и назовите характер движения тела;

4) максимальную высоту подъема, дальность полета и модуль перемещения;

5) радиус кривизны в верхней точке траектории.

2. Вычислите ускорения тел и силы натяжения нитей (рисунок 2.5). Нити невесомые, нерастяжимые, блоки невесомые, .

3. Шар массой 2 кг и радиусом 10 см вращается вокруг оси, проходящей через его центр. Уравнение вращения шара имеет вид: . Найти закон изменения момента сил, действующих на шар, величину их в момент времени 2 с. Вычислите момент инерции шара, если ось вращения будет проходить через половину радиуса.

4. Пять одинаковых шаров, центры которых лежат на одной прямой, находятся на небольшом расстоянии друг от друга. С крайним шаром соударяется такой же шар, имеющий скорость 10 м/с и движущийся вдоль прямой, соединяющей центры шаров. Найти скорость последнего шара, считая соударения шаров абсолютно упругими.

ВАРИАНТ 6

1. Движение тела в поле Земли определяется уравнениями . Вычислите:

1) уравнение траектории движения тела

2) зависимость проекций скорости и ускорения тела от времени , , , ;

3) начальную скорость движения тела;

4) максимальную высоту подъема тела;

5) дальность полета и модуль перемещения тела;

6) радиус кривизны траектории в момент наивысшего подъема;

7) постройте график зависимости для моментов времени ;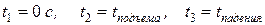

8) назовите характер движения тела.

2. Вычислите ускорения тел и силы натяжения нитей (рисунок 2.6). Нити невесомые, нерастяжимые, блоки невесомые, , внешняя сила .

3. Маховик вращается по закону, выражаемому уравнением 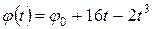, рад. Масса его 5 кг, радиус 10 см. Найти законы, по которым изменяются вращающий момент и мощность. Чему равна мощность и момент сил в момент времени ?

4. Идеально гладкий шар движется со скоростью 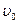и одновременно ударяется с двумя такими же, соприкасающимися между собой шарами и (рисунок 2.7, вид сверху). Найти скорость шаров после соударения, считая соударения шаров абсолютно упругими.

ВАРИАНТ 7

1. Изменения координат материальной точки по двум взаимно перпендикулярным направлениям описывается уравнениями м. Вычислите:

1) зависимость скорости и ускорения от времени;

2) величину скорости, нормального и тангенциального ускорений;

3) уравнение траектории движения точки и характер движения точки, радиус кривизны траектории;

4) модуль перемещения за четверть периода.

2. Вычислите ускорения тел и силы натяжения нитей (рисунок 2.8). Нити невесомые, нерастяжимые, блок невесомый, m₁ =1 кг, m₂ = 2 кг, m₃ = 3 кг коэффициент трения третьего тела о поверхность .

3. Сплошной маховик массой 20 кг и радиусом 120 мм вращается, совершая 600 об/мин. С какой силой нужно прижать к нему тормозную колодку, чтобы он остановился за 3 с, если коэффициент трения равен 0,1? Вычислите также работу торможения и угловое ускорение.

4. Два одинаковых идеально гладких шара радиуса лежат, соприкасаясь друг с другом, на идеально гладкой горизонтальной поверхности. Третий шар из того же материала радиусом движущийся со скоростью по той же плоскости, соударяется одновременно с двумя шарами (рисунок 2.9, вид сверху). Найти скорость третьего шара после соударения, считая соударение шаров абсолютно упругими.

ВАРИАНТ 8

1. Колесо вращается так, что зависимость угла поворота радиуса колеса от времени определяется уравнением . Нормальное ускорение точек, лежащих на ободе колеса к концу второй секунды движения, равно 200 м/с. Вычислите:

1) зависимость линейной и угловой скоростей, линейного и углового ускорений от времени;

2) радиус колеса;

3) угловую скорость и ускорение, тангенциальное и полное ускорение в конце 2-ой секунды движения.

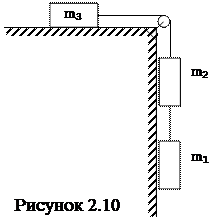
2. Вычислите ускорения тел и силы натяжения нитей (рисунок 2.10). Нити невесомые, нерастяжимые, блок невесомый, , коэффициент трения третьего тела о поверхность .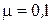

3. С наклонной плоскости, составляющей с горизонтом угол 45° скатывается диск. Длина плоскости 3 м. Пренебрегая трением, Вычислите линейное ускорение центра массы диска, время скатывания и скорость в конце наклонной плоскости.

4. Снаряд при вертикальном выстреле достиг высшей точки полета 3000 м и разорвался на два осколка с массами 3 кг и 2 кг. Осколки продолжают лететь по вертикали: первый – вниз, второй – вверх. Найти скорости осколков через время 2 с после разрыва, если их суммарная энергия в момент взрыва.

ВАРИАНТ 9

1. Движение тела в поле Земли определяется уравнениями . Вычислите:

1) зависимость проекций скорости и ускорения на оси от времени;

2) начальную и конечную скорости движения;

3) уравнения траектории движения тела и постройте график зависимости для моментов времени 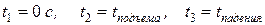, назовите характер движения тела.

4) максимальную высоту подъема, дальность полета и модуль перемещения;

5) радиус кривизны в верхней точке траектории.

2. Вычислите ускорения тел и силы натяжения нитей (рисунок 2.11). Нити нерастяжимые и невесомые, блок невесомый, , коэффициент трения третьего тела о поверхность , внешняя сила .

3. К ободу однородного шара радиусом 0,1 м приложена постоянно касательная сила 50 Н. При вращении на шар действует сила трения, момент которой 4 Н ּ м. Вычислите массу шара, если известно, что он вращается с постоянным угловым ускорением 80 рад/с.

4. Снаряд выпущен под углом к горизонту и в верхней точке траектории, соответствующей высоте 100 м, разорвался на две части массами 1 кг и 1,5 кг. Скорость снаряда в этой точке до разрыва была равна 100 м/с. Скорость большего осколка совпала по направлению со скоростью снаряда и стала равной 250 м/с. Вычислите расстояние между точками падения осколков на Землю. Сопротивлением воздуха пренебречь.

ВАРИАНТ 10

1. Тело движется в поле Земли согласно уравнениям 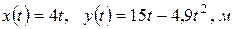. Вычислите:

1) зависимость проекций скорости и ускорения на оси от времени;

2) время движения;

3) запишите уравнение траектории и назовите характер движения;

4) начертить график зависимости:

5) полное ускорение, начальную и конечную скорости движения, а также модуль перемещения тела.

2. Вычислите ускорения тел и силы натяжения нитей (рисунок 2.12). Массы тел , коэффициент трения третьего тела о поверхность , внешняя сила . Нити невесомые, нерастяжимые, блок невесомый.

3. Диск, массой 300 г катится с линейной скоростью 3 м/с по горизонтальной плоскости, а потом вкатывается вверх по наклонной плоскости. Вычислите высоту, на которую он вкатится. Мгновенная ось, относительно которой он вращается в данный момент времени, есть точка соприкосновения диска с плоскостью.

4. Какую минимальную горизонтальную скорость надо сообщить шару, чтобы он сделал полный оборот в вертикальной плоскости? Шар подвешен на жестком невесомом стержне длиной 0,4 м.

ВАРИАНТ 11

1. Диск вращается так, что зависимость угла поворота диска от времени определяется уравнением: . Нормальное ускорение точек, лежащих на ободе колеса к концу второй секунды движения равно 250 м/с². Вычислите:

1) зависимость линейных и угловых скоростей и ускорений от времени;

2)радиус диска;

3)угловую скорость и ускорение, тангенциальное и полное ускорение в конце второй секунды движения.

2. Вычислите ускорения тел и силы натяжения нити (рисунок 2.13). Нити невесомые, нерастяжимые, блок невесомый, массы тел .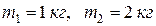

3. Сплошной шар массой 1,5 кг и радиусом 0,05 м, вращается вокруг оси, проходящей через его центр. В точке, наиболее удаленной от оси вращения, на шар действует сила касательная к поверхности. Угол поворота шара меняется по закону: . Вычислите величину силы, тормозящий момент силы, время равнозамедленного движения и кинетическую энергию в начале движения.

4. Какую минимальную горизонтальную скорость надо сообщить шару, чтобы он сделал полный оборот в вертикальной плоскости? Шар подвешен на невесомой нерастяжимой нити длиной 0,4 м.

ВАРИАНТ 12

1. Уравнение координаты материальной точки имеет вид: . Вычислите:

1) зависимость скорости и ускорения от времени;

2) максимальные значения координаты, скорости и ускорения точки;

3) начертить графики зависимости , , ;

4) моменты времени, при которых координата, скорость и ускорение будут максимальны.

2. Вычислите ускорение тел и силу натяжения нити (рисунок 2.14). Нити невесомые, нерастяжимые, блок невесомый, массы тел 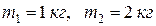, внешняя сила .

3. Цилиндр массой 5 кг и радиусом 15 см вращается вокруг оси, проходящей через его центр. Уравнение вращения цилиндра имеет вид: . Найти закон изменения момента сил, действующих на цилиндр, их величину в момент времени 3 с. Вычислить момент инерции цилиндра, если ось вращения будет проходить по его поверхности.

4. Пуля массой 10 г, летевшая со скоростью 600 м/с, попала в баллистический маятник (рисунок 2.15) массой 5 кг и застряла в нем. На какую высоту поднимется маятник?

ВАРИАНТ 13

1. Движение тела в поле тяжести Земли описывается уравнением . Вычислите:

1) зависимость скорости и ускорения тела от времени;

2) время подъема и время падения тела на Землю;

3) начальную скорость бросания и конечную скорость падения;

4) начертите графики зависимостей , , ;

5) назвать характер движения тела;

6) координату в начальный момент времени, ее физический смысл.

2. Вычислите ускорение тел и силу натяжения нити (рисунок 2.16). Нить невесомая, нерастяжимая, блок невесомый, массы тел 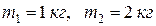, внешняя сила .

3. Сплошной шар массой 5 кг и радиусом 10 см вращается, совершая 120 об/мин. С какой силой нужно прижать к нему тормозную колодку, чтобы он остановился за 2 с, если коэффициент трения равен 0,5? Вычислите также работу, совершаемую при торможении шара и его угловое ускорение.

4. В баллистический маятник массой М = 5 кг попала пуля массой m = 10 г и застряла в нем. Найти скорость пули, если маятник, отклонившись после удара, поднялся на высоту 10 см?

ВАРИАНТ 14

1. Тело движется так, что зависимость координаты от времени определяется уравнением: 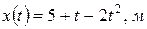. Вычислите:

1) зависимость скорости и ускорения тела от времени;

2) среднюю скорость за третью секунду и за 3 секунды;

3) путь и перемещение за 5 сек;

4) начертить графики зависимости , , ;

5) назвать характер движения тела.

2. Вычислите ускорения тел и силы натяжения нитей (рисунок 2.17). Нити невесомые и нерастяжимые, блок невесомый, .

3. С наклонной плоскости, составляющей с горизонтом угол 60°, скатывается обруч. Длина плоскости 6 м. Пренебрегая трением, вычислите линейное ускорение центра масс обруча, время скатывания и скорость в конце наклонной плоскости.

4. Два груза массами m₁ = 10 кг и m₂ = 15 кг подвешены на нерастяжимых невесомых нитях длиной 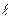= 2 м каждая, так, что грузы соприкасаются между собой. Меньший груз отклонен на угол 60° и выпущен. Вычислите высоту, на которую поднимутся оба груза после удара. Удар абсолютно неупругий.

ВАРИАНТ 15

1. Материальная точка движется в поле Земли согласно уравнениям . Вычислите:

1) зависимость проекций скорости и ускорения на оси 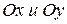от времени;

2) время движения точки;

3) запишите уравнение траектории и назовите характер движения материальной точки;

4) начертить график зависимости ;

5) полное ускорение, начальную и конечную скорости движения, а также модуль перемещения.

2. Вычислите ускорения тел и силы натяжения нитей (рисунок 2.18). Нити невесомые и нерастяжимые, блок невесомый, массы тел , внешняя сила .

3. К ободу однородного цилиндра радиусом 0,3 м приложена постоянно касательная сила 150 Н. При вращении на диск действует сила трения, момент которой 6 Нּм. Вычислите массу тела, если известно, что он вращается с постоянным угловым ускорением 150 рад/с², а также кинетическую энергию в начальный момент времени.

4. Два шара массами 2 кг и 3 кг движутся соответственно со скоростями υ₁ = 8 м/с, υ₂ = 4 м/с. Первый шар нагоняет второй. Вычислите теплоту, выделившуюся при абсолютно неупругом ударе шаров.

ВАРИАНТ 16

1. Движение тела в горизонтальном и вертикальном направлениях в поле Земли определяется уравнениями 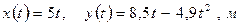. Вычислите:

1) зависимость проекций скорости и ускорения (на оси Х и У) от времени;

2) начальную скорость тела;

3) полное ускорение в верхней точке траектории, а также радиус кривизны в этой точке;

4) время подъема тела и время его движения;

5) уравнение траектории движения тела и характер движения;

6) начертите график зависимости для моментов времени ;

7) дальность полета и модуль перемещения тела.

2. Вычислите ускорения тел и силы натяжения нитей (рисунок 2.19). Нити невесомые и нерастяжимые, блок невесомый, массы тел 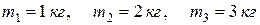, внешняя сила .

3. Обруч массой 1 кг катится с линейной скоростью 5 м/с по горизонтальной плоскости, а потом вкатывается вверх по наклонной плоскости. Вычислите высоту, на которую он вкатывается. Мгновенная ось, относительно которой обруч вращается в данный момент времени, есть точка соприкосновения обруча с плоскостью.

4. Два шара массами 2 кг и 3 кг движутся со скоростями 8 м/с и 4 м/с навстречу друг другу. Вычислите теплоту, выделившуюся при абсолютно неупругом ударе шаров.

ВАРИАНТ 17

1. Уравнение координаты материальной точки имеет вид . Вычислите:

1) зависимость скорости и ускорения от времени;

2) максимальную координату, скорость и максимальное ускорение;

3) начертите графики зависимости для моментов времени ;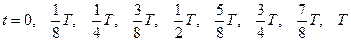

4) назовите характер движения точки;

5) моменты времени, при которых координата, скорость и ускорения будут максимальны.

2. Вычислите ускорения тел и силы натяжения нитей (рисунок 2.20). Нити невесомые и нерастяжимые, , внешняя сила , коэффициенты трения тел о поверхность .

3. Сплошной диск массой 0,5 кг и радиусом 0,1 м вращается вокруг оси, проходящей через его центр. В точке, наиболее удаленной от оси вращения, на диск действует сила, касательная к поверхности. Угол поворота диска меняется по закону: . Вычислите величину силы, тормозящий момент силы, время равнозамедленного движения и кинетическую энергию в начале движения.

4. Тело скользит без начальной скорости с высоты 2 м по наклонной плоскости, угол наклона которой равен 30°. После спуска тело попадает на горизонтальную поверхность, коэффициент трения тела о наклонную плоскость и горизонтальную поверхность 0,3. Какое расстояние пройдет тело по горизонтальной поверхности до остановки.

ВАРИАНТ 18

1. Зависимости координат материальной точки по двум взаимно перпендикулярным направлениям описывается уравнениями:

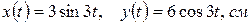Вычислите: 1) зависимость скорости и ускорения от времени;

2) модули скорости и ускорения в момент времени ;

3) максимальную скорость точки;

4) уравнение траектории движения точки

5) постройте график зависимости и определите координаты точек траектории, в которых скорость точки наибольшая и наименьшая. Изобразите их на графике;

6) назовите характер движения точки.

2. Вычислите ускорения тел и силы натяжения нитей (рисунок 2.21). Нити невесомые и нерастяжимые, , внешняя сила , коэффициенты трения тел о поверхность .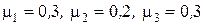

3. Диск массой 5 кг и радиусом 10 см вращается вокруг оси, проходящей через его центр. Уравнение вращения диска имеет вид . Найти закон изменения момента сил, действующего на диск. Вычислите момент сил в момент времени 4с. Вычислить момент инерции диска, если ось вращения будет проходить через половину радиуса.

4. Двум одинаковым телам сообщили равные скорости, направленные под одним и тем же углом 30° к горизонту. Одно тело находится после броска в свободном полете, другое движется без трения по прямой трубе (поставленной под углом ). Какое тело поднимется на большую высоту? Чему равно отношение высот подъема?

ВАРИАНТ 19

1. Зависимость координат материальной точки по двум взаимноперпендикулярным направлениям описывается уравнениями: . Вычислите: 1) зависимость скорости и ускорения от времени;

2) модули скорости и ускорения в момент времени ;

3) максимальную скорость точки;

4) уравнение траектории движения точки

5) постройте график зависимости и определите координаты точек траектории, в которых скорость точки наибольшая и наименьшая, изобразите их на графике.

2. Вычислите ускорение тел и силу натяжения нити (рисунок 2.22). Нить невесомая и нерастяжимая, , коэффициенты трения тел о поверхность , угол внешняя сила .

3. Цилиндр массой 1 кг движется с линейной скоростью 3 м/с по горизонтальной плоскости, а потом вкатывается вверх по наклонной плоскости. Вычислите высоту, на которую он вкатится. Мгновенная ось, относительно которой цилиндр вращается в данный момент времени, есть точка соприкосновения цилиндра с плоскостью.

4. На тележку массой 19 кг движущуюся со скоростью 10 м/с, падает кирпич массой 1 кг и остается на тележке. Вычислите, сколько при этом выделится тепла.

ВАРИАНТ 20

1. Движение тела в поле тяжести Земли описывается уравнением:

. Вычислите: 1) зависимость скорости и ускорения от времени;

2) время подъема, начальную скорость и максимальную высоту подъема;

3) время движения;

4) начертить графики зависимости

5) назвать характер движения тела;

6) координату в начальный момент времени, ее физический смысл.

2. Вычислите ускорение тел и силу натяжения нити (см. рисунок 2.22, вариант 19). Нить невесомая и нерастяжимая, , коэффициенты трения тел о поверхность , внешняя сила , угол .

3. Сплошной цилиндр массой 15 кг и радиусом 100 мм вращается, совершая 180 об/мин. С какой силой нужно прижать к нему тормозную колодку, чтобы он остановился за 2 с, если коэффициент трения равен 0,15? Вычислите работу торможения и угловое ускорение.

4. Телу массы 1 кг, лежащему на длинной горизонтальной доске массы 2 кг (рисунок 2.23) сообщили начальную скорость 3 м/с. Какой путь пройдет доска относительно плоскости к тому времени, когда прекратится скольжение тела относительно доски. Коэффициент трения между доской и телом 0,1, а трение между доской и плоскостью отсутствует.

ВАРИАНТ 21

1.Уравнение координаты материальной точки имеет вид: . Вычислите:

1) зависимость скорости и ускорения от времени;

2) максимальную координату, максимальную скорость и максимальное ускорение;

3) начертить графики зависимости для моментов времени от 0 до Т через 1/8 Т;

4) назвать характер движения материальной точки;

5) моменты времени, при которых координата, скорость и ускорения будут максимальны.

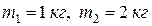2. Вычислите ускорение тел и силу натяжения нити (рисунок 2.24). Нить невесомая, нерастяжимая, , коэффициенты трения тел о поверхность , внешняя сила угол .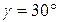

3. Цилиндр вращается по закону, выражаемому уравнением: . Масса его 2,5 кг, радиус 10 см. Найти законы, по которым изменяются вращающий момент силы и мощность. Чему равна мощность и момент сил в момент времени 2 с.

4. По наклонной плоскости с углом наклона с высоты без начальной скорости соскальзывает тело. Достигнув точки , оно начинает подниматься вверх по наклонной плоскости с углом наклона , (рисунок 2.25) Коэффициенты трения тела о плоскости равны . Переход в точке с плоскости на плоскость плавный и гладкий. Найти высоту подъема тела на вторую плоскость.

ВАРИАНТ 22

1.Уравнение траектории материальной точки имеет вид: 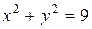, a зависимость координат от времени определяется уравнениями . Вычислите:

1) кинематические характеристики поступательного и вращательного движения точки через 1с после начала движения ;

2) перемещение точки через четверть периода;

3) координаты точки через 1 с, если в начальный момент времени .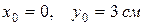

2. Вычислите ускорение тел и силу натяжения нитей (рисунок 2.26). Нить нерастяжимая, блок невесомый, , коэффициент трения первого тела о наклонную плоскость , угол наклонной плоскости .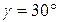

3. С какой силой следует прижать тормозную колодку к колесу, делающему 30 об/с, для его остановки в течение 20 с, если масса колеса распределена по ободу и равна 10 кг, диаметр колеса 20 см? Коэффициент трения между колодкой и ободом колеса 0,5.

4. Акробат падает с высоты 2,4 м на туго натянутую упругую предохранительную сетку. На какой предельной высоте над полом надо натянуть сетку, чтобы акробат не ударился о пол при падении? Известно, что спокойно лежащий акробат дает провисание 0,1 м.

ВАРИАНТ 23

1. Зависимость координат (X, У) материальной точки по двум взаимно-перпендикулярным направлениям описывается уравнениями . Вычислите:

1) зависимость скорости и ускорения от времени;

2) модуль скорости и ускорения в момент времени ;

3) максимальную скорость и ускорение точки;

4) уравнение траектории движения точки, построить график и вычислите характер движения тела);

5) координаты точек траектории, в которых скорость точки будут наибольшей и наименьшей, изобразите их на графике.

2. Вычислите ускорение тел и силу натяжения нити (рисунок 2.27). Нить нерастяжимая, блок невесомый, , коэффициент трения первого тела о наклонную плоскость , внешняя сила , угол наклонной плоскости .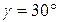

3. Маховик в форме сплошного диска имеет массу 50 кг и радиус 0,2 м. Он раскручен до 8 об/с и затем предоставлен самому себе. Под влиянием силы трения, приложенной по касательной к ободу, маховик останавливается. Вычислите силу трения, считая её постоянной, если маховик останавливается через 50 с и до полной остановки делает 200 оборотов.

4. Два одинаковых шарика соединены невесомым стержнем длиной . Система расположена на горизонтальной плоскости и приведена во вращение так, что ее центр покоится. Сколько оборотов сделает система? Начальная скорость каждого шарика , коэффициент трения о плоскости .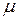

ВАРИАНТ 24

1. Уравнение траектории материальной точки имеет вид , а зависимость координат от времени определяется уравнениями . Вычислите:

1) кинематические характеристики поступательного и вращательного движения материальной точки через 1 с после начала движения ;

2) перемещение точки через четверть периода;

3) координаты точки через 1 с, если в начальный момент времени .

2. Вычислите ускорение тел и силу натяжения нити (рисунок 2.28).

Нить нерастяжимая, блок невесомый, , коэффициент трения первого тела о плоскость , внешняя сила 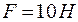, угол наклонной плоскости .

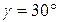3. Карандаш длиной 15 см, поставленный вертикально, падает на стол. Какую угловую и линейные скорости будут иметь в конце падения: 1) середина карандаша? 2) верхний его конец? Считать, что трение настолько велико, что нижний конец карандаша не проскальзывает.

4. Небольшое тело, двигаясь с горизонтальной скоростью на высоте , распалось на две части одинаковой массы. Одна часть упала на землю через время после распада. Вторая часть упала позднее. Сопротивлением воздуха пренебречь. Через какое время после распада вторая часть упала на землю?

ВАРИАНТ 25

1. Движение тела в поле тяжести Земли описывается уравнением . Вычислите:

1) зависимость скорости и ускорения от времени;

2) время подъема, начальную скорость и максимальную высоту подъема;

3) время движения;

4) начертить графики зависимости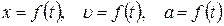

5) назвать характер движения тела;

6) координату в начальный момент времени, ее физический смысл.

2. Вычислите ускорение тел и силу натяжения нити (рисунок 2.29).

Нить нерастяжимая, блок невесомый, , коэффициент трения первого тела о поверхность плоскости 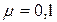, угол наклонной плоскости .

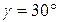3. Сколько времени будет скатываться без скольжения обруч с наклонной плоскости длиной 2 м и высотой 15 см.

4. Два пластилиновых шара, массы, которых относятся как 1:3, подвешены на одинаковых нитях и касаются друг друга. Шары симметрично развели в разные стороны и одновременно отпустили. При ударе они слиплись. Какая часть кинетической энергии шаров при этом превратилась в тепло?

Не нашли, что искали? Воспользуйтесь поиском: