Решение задачи 5.2.

= =

Несмотря на то, что скобки мы раскрыли похожим образом, дальше будет существенное отличие, т.к. свойства векторного произведения совсем другие, чем скалярного. Так, , но . Кроме того, чтобы объединить в одно слагаемое, здесь надо сначала у одной из них сменить знак.

= =

= . Модуль векторного произведения и это площадь параллелограмма, где эти векторы являются сторонами, поэтому далее можно продолжить так:

= = = 50. Ответ. 50.

Задача 6. Решить систему уравнений

Решение.

Построим расширенную матрицу системы и преобразуем её.

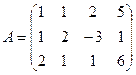
чтобы обнулились коэффициенты ниже левого верхнего угла, то есть чтобы исчезла переменная из всех уравнений кроме первого, надо:

а) из 2-й строки вычесть 1-ю;

б) из 3-й строки вычест удвоенную 1-ю.

=

Теперь, чтобы обнулить ниже чем , нужно к 3-й строке просто прибавить 2-ю, так как знаки там противоположны. При этом структуру из нулей, которые уже получились слева, мы на последующем шаге всё равно никак не испортим, ведь там к 0 будет прибавляться 0 либо вычитаться 0, то есть ступенчатая структура там уже всё равно будет сохраняться.

=

Когда в основной матрице уже получена треугольная структура, снова перепишем в виде системы

В первом уравнении 3 неизвестных, а в каждом следующем всё меньше и меньше, а в последнем вообще только одна неизвестная. Именно этой цели мы и хотели добиться, приводя к треугольному виду: из последнего уравнения можно теперь сразу выразить . Затем с этой информацией мы поднимаемся в предпоследнее уравнение, где две неизвестных, впрочем, одна из них уже известна.

.

А теперь уже две последних неизвестных стали известны, и с этой информацией поднимаемся в 1-е уравнение, подставляя туда и . Итак, .

Ответ. =2, =1, =1.

Можно ответ записать и в виде вектора: .

Задача 7. Найти собственные числа и векторы .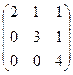

Решение. сводится к уравнению

, корни которого .

Найдём собственные векторы.

. Вычтем 2 по диагонали, получим систему уравнений

то есть .

Из этих уравнений следует, что , про нет информации, это свободная переменная. ФСР: вектор (1,0,0).

. Вычтем 3 по диагонали, получим систему уравнений

то есть .

Из этих уравнений следует , ФСР: вектор (1,1,0).

Базисный минор здесь во 2 и 3 столбцах, так что могло считаться свободной переменной.

. Вычтем 4 по диагонали, получим систему уравнений

то есть .

Базисный минор можно найти, например, в левом верхнем углу, тогда считаем свободной переменной и все остальные выразим именно через неё. Из 2-го , а затем из 1-го , то есть .

ФСР: вектор (1,1,1).

Ответ.

Собст. число собст. вектор (1,0,0),

собст. число собст. вектор (1,1,0)

собст. число собст. вектор (1,1,1).

Задача 8.1. Построить уравнение прямой (на плоскости) по точке 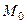с координатами (1,2) и перпендикуляру 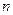(3,5).

Решение. Возьмём произвольную точку с координатами . Если она принадлежит этой прямой, то вектор 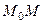, координаты которого равны перпендикулярен вектору .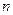

Таким образом, скалярное произведение векторов и (3,5) есть 0. Тогда , приводя подобные, получаем .

Ответ. .

Задача 8.2. Построить уравнение прямой (на плоскости) по точке 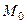с координатами (1,2) и направляющему l (3,5).

Решение. Возьмём произвольную точку с координатами . Если она принадлежит этой прямой, то вектор 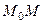а именно коллинеарен вектору l (3,5). Таким образом, их координаты пропорциональны: . Это уравнение называется каноническим. Приведём к обычному уравнению, для этого домножим на константы. , то есть что сводится к .

Замечание. Нормаль к полученной прямой - вектор . Вообще говоря, мы могли бы сразу перейти от направляющего вектора к нормали (поменять координаты и у одной из них сменить знак), а потом уже строить уравнение по нормали, как в прошлом методе.

Ответ. .

Задача 8.3. Построить уравнение плоскости, проходящей через точку А (1,2,3) перпендикулярно вектору 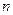(1,4,2).

Решение. Для произвольной точки в плоскости, вектор с координатами ортогонален . Их скалярное произведение 0. Тогда , т.е.

.

Ответ. Уравнение плоскости .

Не нашли, что искали? Воспользуйтесь поиском: