Контрольная работа № 3.

9. Предел последовательности

10. Предел функции, с неопределённостью 0/0.

11. Предел функции, 1-й замеч. lim

12. Предел функции, 2-й замеч. lim

Вариант для самостоятельного решения:

9) Вычислить предел

10) Вычислить предел

11) Вычислить предел

12) Вычислить предел

Аналогичные задачи из практических занятий:

Задача 9. Найти предел .

Решение. Здесь неопределённость типа .

Чтобы свести к дроби, и сокращать как в прошлых примерах, надо сначала домножить на «сопряжённое» выражение, то есть такое где вместо разности сумма, это позволит использовать формулу сокращённого умножения .

= =

= .

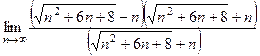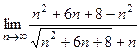Теперь можно сократить на первую степень :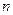

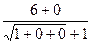= = = = = = 3. Ответ. 3.

Задача 10. Найти предел .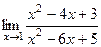

Решение. Способ 1. Тот факт, что при подстановке и в числителе, и в знаменателе даёт значение 0, говорит о том, что множитель присутствует хотя бы один раз. Поэтому найти корни можно даже без дискриминанта.

= = = = = .

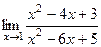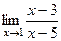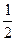Способ 2. (Лопиталя).

= = = = = .

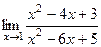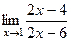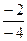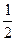Ответ. .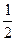

Задача 11.1. Найти предел .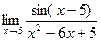

Решение. С помощью преобразований получим в знаменателе такое же выражение, как под знаком синуса в числителе.

= = = = .

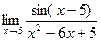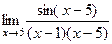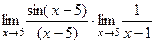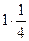Второй предел вообще не содержит неопределённости, а первый это в точности 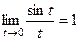если переобозначить .

Ответ. .

Задача 11.2. Найти предел .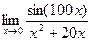

Решение. 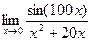= = = 5.

Ответ. 5.

Задача 12. Найти предел .

Решение. Здесь сначала заметим, что основание стремится к 7/7 = 1. А степень к бесконечности. То есть, неопределённость типа и можно использовать 2-й замечательный предел. Сначала выделяем целую часть дроби, то есть 1. Прибавим и отнимем 1, но ту, которую отняли, представим в таком виде, чтобы она объединилась с дробью.

= = =

=

= теперь после 1 следует бесокнечно-малая, которая обращается в 0 при , ведь там числитель . Далее, в степени домножаем обратную к этой дроби, но при этом и её саму тоже, чтобы ничего не изменилось.

= =

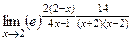
использовали тот факт, что .

Далее, получаем =

= = .

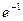Ответ. .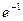

Не нашли, что искали? Воспользуйтесь поиском: