
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Контрольная работа № 4.
1. Функциональные ряды.
2. Ряды Тейлора
3. Ряды Лорана.
4. Ряды Фурье.
Вариант для самостоятельного решения:
1. Найти область сходимости ряда 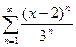 .
.
2. Функцию  разложить в ряд Тейлора по степеням
разложить в ряд Тейлора по степеням  .
.
3. Функцию  разложить в ряд Лорана по степеням
разложить в ряд Лорана по степеням  .
.
4. Найти ряд Фурье для 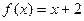 на интервале
на интервале 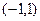 .
.
Аналогичные задачи из практических занятий:
Задача 1.1. Найти область сходимости ряда  .
.
Решение. По признаку Даламбера,  =
= 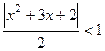 , тогда
, тогда  , что равносильно выполнению одновременно двух неравенств:
, что равносильно выполнению одновременно двух неравенств:  .
.
Для правого неравенства, получаем  , корни
, корни  , оно верно для
, оно верно для 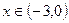 .
.
Для левого неравенства,  , но это выполняется на всей числовой прямой, т.к. корней нет, а ветви этой параболы направлены вверх. Верно для
, но это выполняется на всей числовой прямой, т.к. корней нет, а ветви этой параболы направлены вверх. Верно для  . Пересечением этих двух множеств является интервал
. Пересечением этих двух множеств является интервал  .
.
Также легко заметить, что в граничных точках ряд принимает вид
 , расходится.
, расходится.
Ответ. абсолютно сходится в  .
.
Задача 1.2. Найти область сходимости ряда  .
.
Решение. По признаку Коши,  =
=  , т.е.
, т.е.  , что равносильно
, что равносильно  или
или  . Для граничных точек получаются числовые ряды, для которых нет сходимости (по необходимому признаку).
. Для граничных точек получаются числовые ряды, для которых нет сходимости (по необходимому признаку).
Ответ. абсолютно сходится в  .
.
Задача 2. Разложить в ряд Тейлора:  по степеням
по степеням  .
.
Решение. Разложение на простейшие сначала производится точно так же, как в задаче 8:  . Но здесь центр круга не в 0, а в точке
. Но здесь центр круга не в 0, а в точке  потому что
потому что  . Точки разрыва
. Точки разрыва 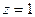 и
и  . Поэтому расстояние до ближайшей точки разрыва равно 2, и круг здесь имеет вид
. Поэтому расстояние до ближайшей точки разрыва равно 2, и круг здесь имеет вид 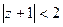 . Он показан на чертеже:
. Он показан на чертеже:
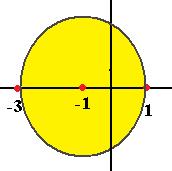
В выражении  сначала надо прибавить и отнять константы, чтобы в знаменателе явно был выделен блок
сначала надо прибавить и отнять константы, чтобы в знаменателе явно был выделен блок  .
.
 =
=  теперь скобку вида
теперь скобку вида  мы не будем раскрывать вплоть до ответа, можно даже переобозначить её через
мы не будем раскрывать вплоть до ответа, можно даже переобозначить её через  (но не обязательно).
(но не обязательно).
Выносим за скобку константу 2 в каждой из дробей.
 . В круге
. В круге 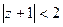 получается, что верно
получается, что верно  то есть там как раз получается такое
то есть там как раз получается такое  , как и надо для сходящейся геометрической прогрессии. Тогда далее
, как и надо для сходящейся геометрической прогрессии. Тогда далее
 =
=  .
.
Здесь в 2 частях индексы меняются синхронно, т.е. можно объединить
 .
.
Ответ.  .
.
Задача 3. Разложить в ряд Лорана  по степеням z
по степеням z
Решение. Точки разрыва  и
и  , центр кольца в 0, значит, кольцо определяется условием
, центр кольца в 0, значит, кольцо определяется условием 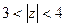 .
.
 =
=  =
=  =
=
 . Можно ещё произвести сдвиг индекса в главной части, чтобы не был индекс 0 в двух частях сразу:
. Можно ещё произвести сдвиг индекса в главной части, чтобы не был индекс 0 в двух частях сразу:
Ответ.  .
.
Задача 4. Разложить 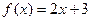 в тригонометрический ряд Фурье на интервале (-1,1).
в тригонометрический ряд Фурье на интервале (-1,1).
Решение. Заметим, что функция 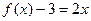 нечётная. То есть, f это сумма нечётной и константы. Таким образом, коэффициенты
нечётная. То есть, f это сумма нечётной и константы. Таким образом, коэффициенты  здесь тоже окажутся равны 0. Надо вычислить
здесь тоже окажутся равны 0. Надо вычислить  и
и 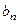 .
.
 =
=  =
=  ,
,  .
.
 . Вычисляем интеграл по частям.
. Вычисляем интеграл по частям.
 ,
,  ,
,  ,
, 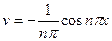 . Тогда
. Тогда
 =
=
 =
=  =
=  =
=  =
= 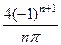 .
.
Ответ. Ряд Фурье:  .
.
Список литературы
I. Пособия кафедры.
1. Л.И.Магазинников, А.Л. Магазинникова. Линейная алгебра. Аналитическая геометрия. Учебное пособие http://edu.tusur.ru/publications/2244
2. Л.И.Магазинников, А.Л.Магазинников. Дифференциальное исчисление. Учебное пособие http://edu.tusur.ru/publications/2246
3. А.А.Ельцов, Т.А.Ельцова. Интегральное исчисление и дифференциальные уравнения http://edu.tusur.ru/publications/2259
4. Л.И.Магазинников. Высшая математика III. Функции комплексного переменного. Ряды. Интегральные преобразования
http://edu.tusur.ru/publications/2258
II. Учебные пособия для 446 групп.
1. Приходовский М.А. Математика (курс лекций, семестр 2, часть 1): Учебное пособие для специальности 09.03.03 «Прикладная информатика в экономике» — Томск: ТУСУР, 2016. — 90 с. http://edu.tusur.ru/publications/6051 2. Приходовский М.А. Математика (курс практических занятий, семестр 2, часть 1): Учебно-методическое пособие для специальности 09.03.03 - Прикладная информатика в экономике — Томск: ТУСУР, 2016. — 78 с. http://edu.tusur.ru/publications/6044 3. Приходовский М.А. Математика (курс лекций, семестр 2 часть 2): Учебное пособие для специальности 09.03.03 - Прикладная информатика в экономике — Томск: ТУСУР, 2016. — 64 с. http://edu.tusur.ru/publications/6077 4. Приходовский М.А. Математика (курс практических занятий, семестр 2, часть 2): Учебно-методическое пособие для специальности 09.03.03 - Прикладная информатика в экономике — Томск: ТУСУР, 2016. — 34 с. http://edu.tusur.ru/publications/6078 5. Приходовский М.А. Математика (курс лекций, семестр 1, часть 1) учебное пособие для специальности 09.03.03 "прикладная информатика в экономике" — Томск: ТУСУР, 2016. — 84 с. http://edu.tusur.ru/publications/6308 6. Приходовский М.А. Математика (курс практических занятий, семестр 1, часть 1) учебное пособие для специальности 09.03.03 "прикладная информатика в экономике" — Томск: ТУСУР, 2016. — 102 с. http://edu.tusur.ru/publications/6307
Не нашли, что искали? Воспользуйтесь поиском: