
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Контрольная работа № 1.
1. Подведение под знак дифференциала, преобразования.
2. Интегрирование по частям.
3. Интегрирование рациональных дробей.
4. Интегрирование иррациональностей и тригонометрических функций.
Варианты для самостоятельного решения:
Вариант 1. Найти неопределённые интегралы:
1.  2.
2. 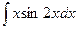 3.
3. 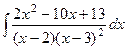 4.
4. 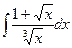
Вариант 2. Найти неопределённые интегралы:
1.  2).
2). 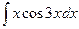 3.
3. 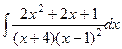 4.
4. 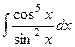
Аналогичные задачи из практических занятий:
Задача 1.1. Вычислить 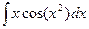 .
.
Решение. 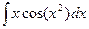 =
=  =
= 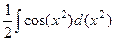 =
=
= 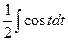 =
= 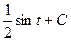 =
= 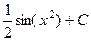 .
.
Ответ. 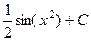 .
.
Задача 1.2. Вычислить 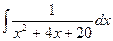 .
.
Решение. Дискриминант знаменателя отрицательный, поэтому здесь невозможно сделать как в прошлой задаче, так как нет корней знаменателя и дробь невозможно свести к виду 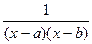 .
.
Но при D < 0 можно выделить полный квадрат:
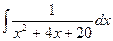 =
=  =
= 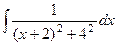 .
.
С помощью замены 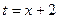 сводится к интегралу:
сводится к интегралу:
 =
= 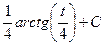 , и далее с помощью обратной замены получаем ответ:
, и далее с помощью обратной замены получаем ответ: 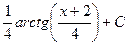 .
.
Ответ. 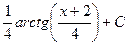 .
.
Задача 2.1. Вычислить 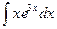 .
.
Решение. Пусть 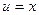 , так надо, чтобы понизилась степень на следующем шаге. Составим таблицу:
, так надо, чтобы понизилась степень на следующем шаге. Составим таблицу:
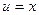
| 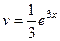
|

| 
|
Тогда 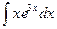 =
= 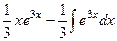 =
= 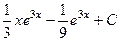 .
.
Ответ. 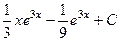 .
.
Задача 2.2. Вычислить 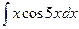 .
.
Решение.
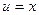
| 
|

| 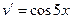
|
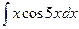 =
=  =
= 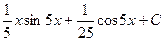 .
.
Ответ. 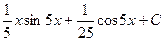 .
.
Задача 3. Вычислить интеграл 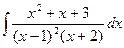 .
.
Решение. Как видим, здесь корень 1 имеет кратность 2. Разложение на простейшие дроби нельзя проводить так, как будто бы здесь три независимых множителя  ,
,  ,
, 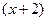 , т.е.
, т.е.  , иначе получится противоречие, ведь общий знаменатель будет содержать всего лишь 1-ю степень
, иначе получится противоречие, ведь общий знаменатель будет содержать всего лишь 1-ю степень  но никак не вторую. Надо степени знаменателя учитывать по возрастающей, до кратности корня, а именно, так:
но никак не вторую. Надо степени знаменателя учитывать по возрастающей, до кратности корня, а именно, так:  .
.
Приведём к общему знаменателю:
 .
.
Числитель этой дроби равен числителю исходной, той, которая была в интеграле:
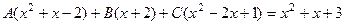 .
.
 , система:
, система:
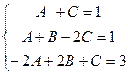 . Построим расширенную матрицу и решим систему уравнений:
. Построим расширенную матрицу и решим систему уравнений:

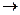
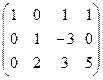
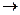
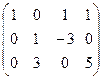 .
.
Система приведена к виду: 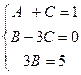
Тогда 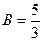 ,
,  ,
, 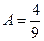 . И теперь интеграл распадается на сумму трёх интегралов:
. И теперь интеграл распадается на сумму трёх интегралов:  .
.
В 1 и 3 слагаемых - как раньше, а вот во 2-м логарифм в ответе не получится, ведь тут уже 2-я а не 1-я степень в знаменателе.
Полезно вспомнить, что 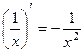 .
.
То есть, интеграл от -2 степени будет содержать -1 степень, и меняется знак.
Ответ.  .
.
Задача 4.1. Вычислить интеграл 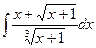 .
.
Решение. Здесь есть корни порядка 2 и 3. Наименьшее общее кратное, НОК(2,3) = 6. Поэтому замена 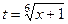 . При этом,
. При этом,
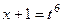 ,
, 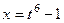 ,
, 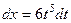 ,
,
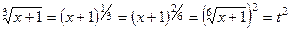 ,
,
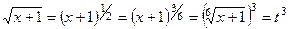 .
.
Тогда 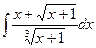 =
=  =
= 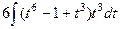 =
=
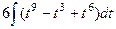 =
=  .
.
Сделаем обратную замену и получим ответ:
Ответ. 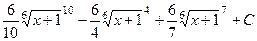 .
.
Задача 4.2. Вычислить интеграл 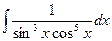 .
.
Решение. Здесь тоже суммарная степень чётная, замена  .
.
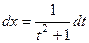 .
. 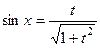 ,
, 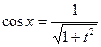 .
.
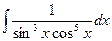 =
= 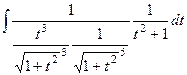 =
=  =
=
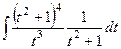 =
=  =
= 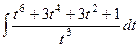
здесь мы воспользовались формулой 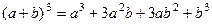 .
.
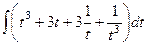 =
=  .
.
После обратной замены получаем ответ:
Ответ.  .
.
Не нашли, что искали? Воспользуйтесь поиском: