Разрешающая способность спектрального прибора.

Условие образования главных максимумов для вогнутой решетки такое же, как и для плоской, т.е. , где d – период решетки; m – порядок спектра; λ – длина световой волны. Основными характеристиками вогнутой дифракционной решетки являются: разрешающая способность, угловая и линейная дисперсия. Угловую дисперсию получим, дифференцируя соотношение. Тогда .

Линейная дисперсия вогнутой решетки равна ,где ρ – радиус кривизны решетки (ρ=250 мм).

Вращая барабан, мы поворачиваем на определенный угол дифракционную решетку. Поворот решетки приводит к перемещению спектра. Если барабан повернуть на N делений, то решетка повернется на угол α. Тогда дифрагированный луч отклонится от первоначального положения на угол 2 α. Общее отклонение дифрагированного луча от первоначального положения нормали составит φ+2α. Таким образом, поворот барабана на Δ N делений пропорционален изменению угла дифракции на Δφ, а величина пропорциональна угловой дисперсии 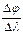. Проведем оценку соотношений Δ N и Δφ. Сканирование спектра осуществляется поворотом дифракционной решетки. При повороте барабана от деления 400 до 730 дифракционная решетка повернется на угол от 13^○33’ до 24^○52’, а дифрагированный луч отклонится на угол, в два раз больший. Тогда . Угловая дисперсия равна 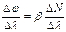. Линейную дисперсию найдем как . Разрешающая способность прибора R равна , где – средняя длина волны, Δλ – расстояние между двумя близко расположенными линиями. Разрешающая способность решетки зависит от числа штрихов решетки N, порядка спектра m и равна .

Не нашли, что искали? Воспользуйтесь поиском: