Механические гармонические колебания

Физическим маятником называется абсолютно твердое тело, совершающее колебание под действием силы тяжести вокруг горизонтальной оси, не проходящей через его центр тяжести.

Математическим маятником называется материальная точка, подвешенная на невесомой, нерастяжимой нити и совершающая колебания под действием силы тяжести.

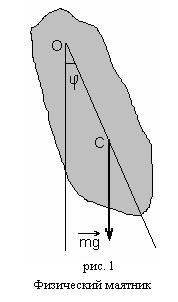На рисунке 1 показано сечение физического маятника плоскостью, перпендикулярной к оси вращения и не проходящей через центр масс 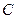. Расстояние равно . При отклонении маятника от

положения равновесия на угол под действием силы тяжести возникает вращательный момент сил 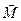, стремящейся вернуть маятник в положение равновесия. Величина момента сил

равна ,

где – масса маятника. При малом угле

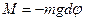(1)

Для вывода закона движения маятника используем основной закон динамики вращательного движения:

(2)

где – момент инерции маятника относительно оси , – угловое ускорение. Спроектировав (2) на положительное направление оси вращения, связанное правилом буравчика с вектором , и подставляя (1) в (2), получим:

.

Поделив на , получим:

Введем обозначение:

(3)

– циклическая частота колебаний; тогда придем к стандартному дифференциальному уравнению гармонических колебаний:

(4)

Его решением является периодическая функция с периодом , которая имеет вид:

(5)

Где 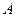– амплитуда колебаний, – начальная фаза колебаний, – фаза колебаний.

Следовательно, при малых углах отклонения маятника угловое отклонение изменяется со временем по гармоническому закону.

Амплитуда – это максимальное значение колеблющейся величины.

Период – время одного полного колебания.

Частота – число колебаний за единицу времени.

Период колебаний физического маятника

(6)

Для математического маятника формулу циклической частоты и периода можно получить из (3) и (6), если рассматривать математический маятник как частный случай физического, у которого вся масса сосредоточена в центре масс 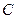на расстоянии от подвеса. Тогда из (6):

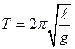(7)

Из сопоставления формул (6) и (7) получается, что математический маятник с длиной 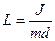будет иметь такой период колебаний, как и данный физический маятник. Величину 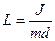называют приведенной длиной физического маятника. Таким образом, приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника.

Не нашли, что искали? Воспользуйтесь поиском: