Связанные электромагнитные колебания

Примером системы с двумя степенями свободы является схема из двух электрических контуров с емкостной связью между ними (рис.13) Величина определяет степень взаимной связи контуров.

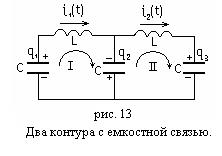
Рассмотрим влияние емкости связи на характеристики результирующего колебания. Полагаем для простоты контуры одинаковыми. Если емкость связи замкнута, контуры взаимно независимы и колебания, например, зарядов на каждой из емкостей 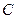описывается уравнением:

(25)

где – собственная частота колебательных контуров. Изменение зарядов описывается гармоническими функциями:

(26)

Если емкость связи отключена, то схема рис. 13 представляет собой единичный колебательный контур с индуктивностью и емкостью , резонансная частота которого равна .

Введение элемента связи меняет характер электрических связей в каждом из контуров. Однако, можно показать, что сложное колебание, происходящее в системе может быть представлено как суперпозиция двух независимых гармонических колебаний, которые получили название нормальных или собственных колебаний системы. Частоты этих колебаний называются нормальными и могут быть не равны собственным частотам контуров, входящих в систему.

Выведем уравнения, описывающие систему связанных электрических контуров (рис. 13). В силу закона сохранения электрического заряда . Законы Кирхгофа для контуров I и II, направление обхода которых показано на рис. 13:

(27)

где , , -–напряжения на емкостях с зарядами соответственно.

Для уменьшения числа неизвестных в системе уравнений (27) используем соотношения: , .

Система уравнений (27) принимает вид:

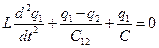
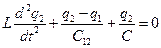(28)

Систему связанных уравнений (28) относительно функций времени можно преобразовать в два независимых уравнения, это позволяет упростить решение задачи. Для этого каждое уравнение системы (28) разделим на и вначале сложим, потом вычтем:

(29)

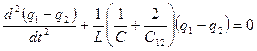
Решение уравнений (29) может быть найдено в виде:

(30)

где амплитуды колебаний для удобства обозначены 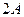и , частоты колебаний определяются формулами:

(31)

Используя (6) можно найти искомые функции времени для зарядов:

(32)

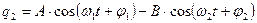
Таким образом, колебания зарядов в каждом из контуров может быть представлено в виде суммы двух гармонических колебаний с частотами и , которые называются нормальными. Значения переменных величин в произвольный момент времени определяются начальными условиями . Выпишем начальные значения зарядов и токов, используя (32) и определение силы тока :

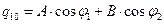
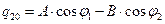
(33)

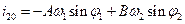
Рассмотрим различные способы возбуждения колебаний в системе.

Синфазные колебания. Пусть в начальный момент времени заряды на емкостях равны, а знаки соответствуют рис. 13, то есть

.

Этот случай соответствует синфазным колебаниям: в обоих контурах происходят колебания с нормальной частотой , совпадающей с собственной частотой каждого из контуров . В этом случае в произвольный момент времени заряд на емкости и ток через элемент связи не протекает. Колебания происходят так, как если бы отсутствовал участок цепи, содержащий емкость связи (рис. 14).

Антифазные колебания. Пусть в начальный момент времени заряды на емкостях 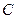одинаковы, причем верхние пластины заряжены положительно, то есть . В этом случае токи равны по величине и противоположны по направлению (рис. 15).

Биения. Пусть в начальный момент времени заряжена только одна из емкостей 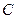, то есть . Учитывая (33), а также для упрощения полагая начальные фазы , получим:

,

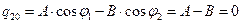то есть . Тогда в любой момент времени:

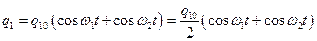
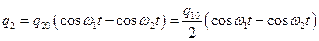
Используя формулу суммы косинусов, получим решение в виде:

(34)

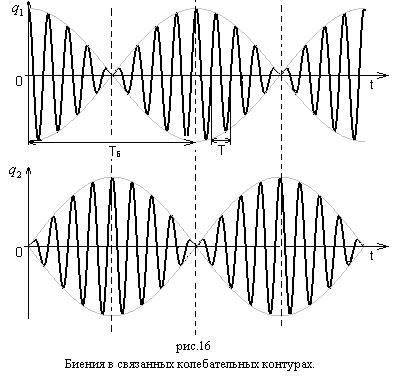
Из (34) видно, что колебания зарядов происходят с частотой , а амплитуда колебаний меняется при этом с частотой . Зависимость зарядов на конденсаторах от времени показана на рис. 16.

В начальный момент времени вся энергия сосредоточена в первом колебательном контуре, в котором происходят колебания с частотой . За счет элемента связи вся энергия постепенно передается во второй колебательный контур до тех пор, пока вся энергия не будет сосредоточена во втором колебательном контуре. Затем начинается обратный переход энергии в первый контур. Время перехода энергии из первого контура во второй и обратно можно получить из уравнения (34):

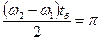
Отсюда частота, с которой колебательные контуры обмениваются энергией, равна:

.

Таким образом, при заряде одной из емкостей в каждом из колебательных контуров осуществляется сложное колебание, характеризуемое периодическими изменениями амплитуды, биения. Биения наблюдаются также при сложении однонаправленных колебаний с близкими частотами (см. лабораторную работу №76).

При слабой связи между контурами частота обмена энергией

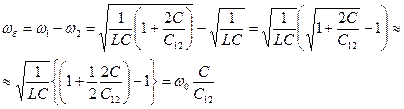
Период биений: ,

Где – период собственных колебаний в контуре.

Аналогичные результаты могут быть получены для токов дифференцируя формулы (8), (10) по времени ; для напряжений на емкостях . Связанные колебания удобно изучать, исследуя токи , напряжения на активных сопротивлениях, специально вводимых в схему. Наличие активных сопротивлений в схеме приводит к затуханию энергии и проявляется в уменьшении амплитуды огибающей (см. рис. 16).

Приложение 2

Не нашли, что искали? Воспользуйтесь поиском: