
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Связанные механические колебания
 В случае двух связанных маятников первая мода возникает, если в системе возбудить синфазные колебания, а другая – при возбуждении антифазных колебаний.
В случае двух связанных маятников первая мода возникает, если в системе возбудить синфазные колебания, а другая – при возбуждении антифазных колебаний.
Найдем частоты этих мод или нормальные частоты.
Для возбуждения синфазных колебаний оба связанных маятника отклоняют на одинаковый малый  угол
угол 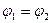 в одну и ту же сторону от положения равновесия (рис. 10). Воспользуемся основным законом вращательного движения вокруг неподвижной оси
в одну и ту же сторону от положения равновесия (рис. 10). Воспользуемся основным законом вращательного движения вокруг неподвижной оси  :
:

или
 (15)
(15)
где  – момент силы тяжести;
– момент силы тяжести;  – момент силы упругости;
– момент силы упругости;  – момент инерции маятника относительно оси
– момент инерции маятника относительно оси  ,
,  – его угловое ускорение. Так как пружина не деформирована, сила упругости, а следовательно, и ее момент
– его угловое ускорение. Так как пружина не деформирована, сила упругости, а следовательно, и ее момент 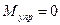 . Тогда равенство (15) в скалярной форме переписывается в виде:
. Тогда равенство (15) в скалярной форме переписывается в виде:
 (16)
(16)
Знак  означает, что момент силы тяжести стремится вернуть маятник в положение равновесия. Так как
означает, что момент силы тяжести стремится вернуть маятник в положение равновесия. Так как  ,
, 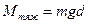 , где
, где  – масса маятника;
– масса маятника;  – плечо силы тяжести, то равенство (16) можно представить в виде:
– плечо силы тяжести, то равенство (16) можно представить в виде:
 (17)
(17)
 , а т. к. угол
, а т. к. угол  мал, то
мал, то  и
и 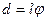 , и (17):
, и (17):
 (18)
(18)
Разделив обе части этого равенства на  , получим дифференциальное уравнение гармонического колебания для величины
, получим дифференциальное уравнение гармонического колебания для величины  :
:
 (19)
(19)
где, очевидно,  – есть квадрат циклической частоты синфазных колебаний. Подставив значение
– есть квадрат циклической частоты синфазных колебаний. Подставив значение 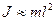 , где
, где  – длина маятника, получим
– длина маятника, получим 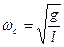 , следовательно, частота синфазных колебаний:
, следовательно, частота синфазных колебаний:
 (20)
(20)
Рассмотрим антифазные колебания маятников, для чего разведем маятники в противоположные стороны на один и тот же небольшой угол 
 . При этом пружина деформируется на величину
. При этом пружина деформируется на величину  (рис. 11).
(рис. 11).
Теперь кроме силы тяжести на маятник будут действовать силы упругости:  .
.
 В скалярной форме уравнение (15) имеет вид:
В скалярной форме уравнение (15) имеет вид: 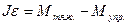 (21)
(21)
Так как  ,
,
где  – расстояние от оси
– расстояние от оси  до связи (пружины);
до связи (пружины);
 – жесткость пружины. При малом уголе
– жесткость пружины. При малом уголе 
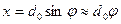 . Равенство (21) перепишется в виде:
. Равенство (21) перепишется в виде:
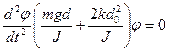 (22)
(22)
Получили дифференциальное уравнение антифазных колебаний.
Здесь 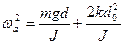 , или учитывается, что
, или учитывается, что 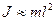 ,
,  – циклическая частота антифазных колебаний, а частота антифазных колебаний:
– циклическая частота антифазных колебаний, а частота антифазных колебаний:
 (23)
(23)
Таким образом, в рассмотренной системе возникают две нормальные моды с частотами 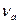 и
и 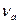 . Изменяя силу связи, т. е.
. Изменяя силу связи, т. е.  и
и  , можно получить очень близкие по частоте две нормальные моды. Если систему привести в движение произвольным образом, возникает сложное движение, которое будет суперпозицией двух близких мод:
, можно получить очень близкие по частоте две нормальные моды. Если систему привести в движение произвольным образом, возникает сложное движение, которое будет суперпозицией двух близких мод: 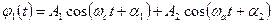 .
.
Положим начальные фазы 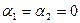 ; если частоты складываемых колебаний близки, т. е.
; если частоты складываемых колебаний близки, т. е. 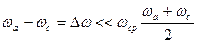 , то возникают так называемые биения. Эффект биения будет наибольшим, если
, то возникают так называемые биения. Эффект биения будет наибольшим, если  . Тогда, используя формулу суммы косинусов
. Тогда, используя формулу суммы косинусов  , получим уравнение биения:
, получим уравнение биения:
 (23)
(23)
где  – амплитуда биения,
– амплитуда биения, 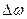 – циклическая частота биений, а
– циклическая частота биений, а  – период биения.
– период биения.
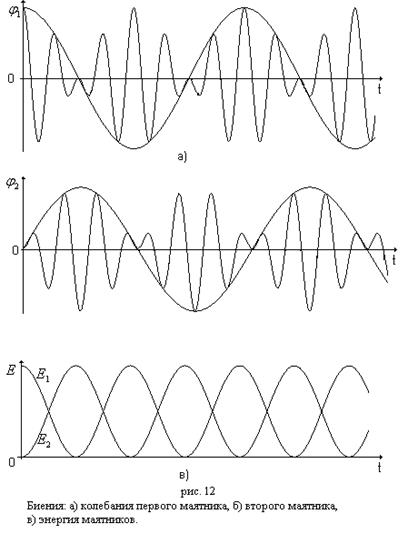
Графически биение 1-го маятника изображены на рис. 12а. Для возбуждения биения отклоним один маятник на 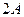 , а второй будем удерживать в нулевой точке. Затем одновременно отпустим оба маятника. Амплитуда колебаний (а, следовательно, и энергия
, а второй будем удерживать в нулевой точке. Затем одновременно отпустим оба маятника. Амплитуда колебаний (а, следовательно, и энергия 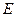 ) первого маятника уменьшается, а второго – возрастает (см. рис. 12б.). Через
) первого маятника уменьшается, а второго – возрастает (см. рис. 12б.). Через 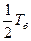 первый маятник остановится, а второй будет иметь амплитуду
первый маятник остановится, а второй будет иметь амплитуду 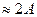 . При этом энергия колебаний переходит от одного маятника к другому полностью. Этот процесс будет периодически повторятся. Один полный оборот энергии от первого маятника ко второму и опять к первому и представляет одно биение (рис. 12в). Очевидно, что этот полный оборот энергии колебаний происходит за время, равное периоду биения
. При этом энергия колебаний переходит от одного маятника к другому полностью. Этот процесс будет периодически повторятся. Один полный оборот энергии от первого маятника ко второму и опять к первому и представляет одно биение (рис. 12в). Очевидно, что этот полный оборот энергии колебаний происходит за время, равное периоду биения 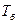 . Если
. Если  – циклическая частота биения, то частота биения:
– циклическая частота биения, то частота биения:
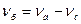 (24)
(24)
Не нашли, что искали? Воспользуйтесь поиском: