РЕЛАКСАЦИОННЫЕ КОЛЕБАНИЯ

В колебательном контуре, содержащем индуктивность и емкость, есть два накопителя энергии. При колебаниях энергия электрического поля конденсатора переходит в энергию магнитного поля катушки индуктивности и обратно.

Встречаются, однако, колебательные системы, содержащие всего один накопитель энергии. Рассмотрим в качестве примера электрическую цепь, содержащую конденсатор и сопротивление.

Разряд конденсатора через сопротивление представляет собой апериодический процесс. Разряду можно, однако, придать периодический характер, возобновляя разряд конденсатора через постоянные промежутки времен с помощью ключа .

Колебания в этом случае являются совокупностью двух апериодических процессов – процесса зарядки конденсатора и его разрядки. Такие колебания называются релаксационными.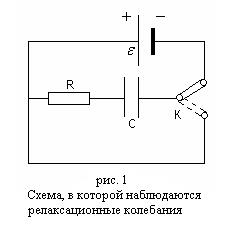

Рассмотрим вначале процесс зарядки конденсатора (рис. 1). Обозначим 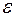– э. д. с. источника, через 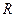– сопротивление цепи (включая и внутреннее сопротивление источника). Применяя к контуру закон Кирхгофа, получим

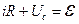(1)

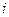– мгновенное значение силы тока: ,

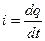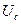– мгновенное значение напряжения на конденсаторе: ,

где 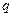– заряд конденсатора.

Из написанных трех равенств мы можем исключить две из трех переменных величин 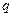, , 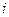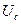. Исключим 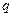и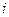

;

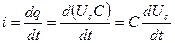Тогда из уравнения (1)

,

,

.

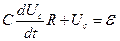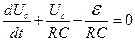Введем новую переменную 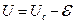, при этом 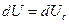, тогда

.

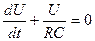Мы получили однородное дифференциальное уравнение первого порядка. Решим его, применив метод разделения переменных:

,

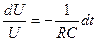проинтегрируем: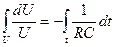

.

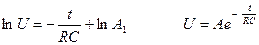Постоянная интегрирования 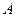зависит от начального условия. Положим, что мы начинаем отсчет времени с момента замыкания цепи. Тогда начальное условие имеет вид:

.

Это дает .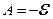

Возвращаясь к прежней переменой 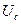, находим окончательное выражение для напряжения на конденсаторе при зарядке конденсатора:

.

В случае разрядки конденсатора (рис. 1) закон Кирхгофа имеет вид:

,

,

,

.

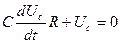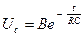Если начало отсчета времени совпадает с началом процесса разрядки, то начальное условие примет вид:

.

В этом случае постоянная интегрирования 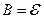и зависимость от времени напряжения конденсатора при разрядке имеет вид:

.

Полученные результаты показывают, что процессы зарядки и разрядки (установление электрического равновесия) происходят не мгновенно, а с конечной быстротой. Для рассмотренного контура, содержащего сопротивление и емкость, быстрота установления зависит от произведения

,

которое имеет размерность времени и называется постоянной времени (временем релаксации) данного контура. Постоянная времени показывает, через какое время после выключения э. д. с. напряжение (а значит, и напряженность поля внутри конденсатора) уменьшается в раза.

В нашей установке роль «ключа», обеспечивающего попеременную зарядку и разрядку конденсатора, играет неоновая лампа.

Неоновая лампа состоит из стеклянного баллона, в который впаяно два электрода – анод и катод в виде металлических пластинок, расположенных на расстоянии 2 – 3 мм. Баллон заполнен неоном при низком давлении (10 – 75 мм рт. ст.).

Основная особенность неоновой лампы заключается в том, что она начинает проводить ток только при определенной разности потенциалов 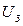между электродами (рис. 2). Если напряжение на электродах лампы 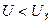ток через лампу не идет, так как неон является диэлектриком.

В этом случае внутреннее сопротивление лампы бесконечно велико. При разности потенциалов 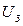происходит пробой диэлектрика – через лампу идет ток. При этом неон светится оранжевым светом, лампа зажигается. 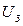называется потенциалом зажигания лампы.

Объясняется этот факт следующим образом. В баллоне всегда присутствует незначительное количество свободных электронов, покинувших металл (электроды лампы). При наложении электрического поля кинетическая энергия этих электронов возрастает за счет работы сил поля. Изменение кинетической энергии осуществляется на пути между последовательными столкновениями электрона с другим электроном или атомом неона. С увеличением напряжения на лампе кинетическая энергия электронов возрастает и достигает величины, достаточной для ионизации молекул газа при соударении (ударная ионизация). Поэтому при постоянном давлении газа разряд наступает при определенном напряжении 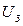– потенциале зажигания.

Потенциал зажигания также зависит от расстояния между электродами, формы электродов, а также от природы и давления газа, заполняющего баллон. После зажигания лампа может гореть уже при более низком напряжении 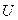, гаснет она при напряжении , которое называется потенциалом гашения.

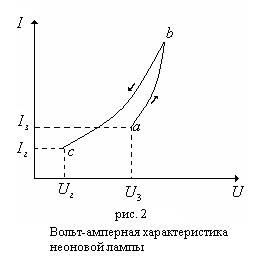
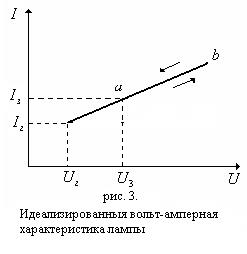
Вольт–амперная характеристика лампы (кривая зависимости тока в лампе от напряжения на ее электродах) имеет вид, представленный на рис. 2.

При малых напряжениях на электродах ток, протекающий через лампу, равен нулю. При вспыхивании лампы ток скачком достигает величины 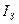. При дальнейшем увеличении напряжения ток в лампе все время возрастает по 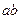. Если уменьшить напряжение, то ток уменьшится по кривой 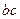, близкой к 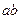, но не совпадающей с ней.

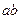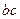Однако для упрощения иногда можно считать, что и совпадают. Такая идеализированная характеристика будет иметь вид, представленный на рис.3. Когда лампа горит, ее внутреннее сопротивление можно оценить по этой идеализированной характеристике.

,

но 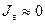, поэтому .

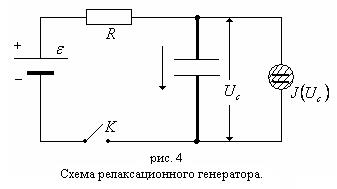Рассмотрим, как происходит колебательный процесс в схеме с неновой лампой. На рис. 4 представлена принципиальная схема релаксационного генератора.

Пусть вначале опыта ключ 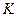разомкнут и . Замкнем ключ 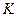. Конденсатор 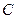начинает заряжаться через сопротивление 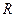, напряжение 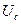возрастает. Как только оно достигает напряжения зажигания 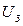лампа начинает проводить ток, причем прохождение тока через лампу сопровождается разрядкой конденсатора. Во время горения лампы конденсатор разряжается и напряжение в нем падает. Когда оно достигает «напряжения гашения», лампа перестает проводить ток и конденсатор вновь начинает заряжаться. Кривая напряжения на конденсаторе изображена на рис. 5. Амплитуда колебаний равна .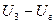

Вычислим период релаксационных колебаний. Полное время колебания 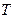состоит из суммы времени зарядки 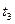и времени разрядки 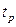. Обычно сопротивление 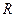выбирают большим, существенно превосходящем сопротивление зажженной лампы. В этом случае (которым мы и ограничимся) 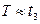. Во время зарядки конденсатора лампа не горит 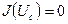и на основании закона Кирхгофа:

.

Будем отсчитывать время с момента гашения лампы, так что при 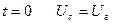(рис. 3). Тогда

.

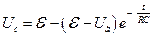В момент зажигания .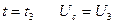

;

;

;

,

.

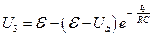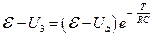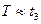Развитая выше теория является приближенной. Следует иметь в виду, что мы полностью пренебрегли паразитными емкостями и паразитными самоиндукциями схемы. Не рассматривали также процессы разряда и деионизации при затухании. Теория справедлива в тех случаях, когда в схеме установлена достаточно большая емкость 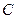и когда период колебаний существенно больше времени развитии разряда и деионизации (практически секунды).

Приложение 3

Не нашли, что искали? Воспользуйтесь поиском: