
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Вынужденные электромагнитные колебания
Вынужденными называются такие колебания, которые происходят в системе под влиянием внешнего периодического воздействия.
Рассмотрим процессы, протекающие в электрическом колебательном контуре, присоединенном к внешнему источнику, ЭДС которого изменяется по гармоническому закону:
 (25)
(25)
 – амплитуда внешней ЭДС,
– амплитуда внешней ЭДС,  – ее циклическая частота. Схема контура представлена на рис. 5.
– ее циклическая частота. Схема контура представлена на рис. 5. 
Обозначим через  напряжение на конденсаторе, а через
напряжение на конденсаторе, а через  – силу тока в контуре. В этом контуре кроме ЭДС действует еще
– силу тока в контуре. В этом контуре кроме ЭДС действует еще 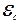 – ЭДС самоиндукции, прямо пропорциональная скорости изменения силы тока в контуре:
– ЭДС самоиндукции, прямо пропорциональная скорости изменения силы тока в контуре: 
Для вывода дифференциального уравнения возникающих в таком контуре колебаний используем второй закон Кирхгофа:
 (26)
(26)
Так как напряжение на сопротивлении 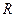 по закону Ома
по закону Ома  , а сила тока есть заряд протекающий за единицу времени через поперечное сечение проводника:
, а сила тока есть заряд протекающий за единицу времени через поперечное сечение проводника:  , то
, то  .
.
Напряжение  на конденсаторе, как следует из определения электроемкости
на конденсаторе, как следует из определения электроемкости 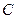 , прямо пропорционально заряду на обкладках конденсатора:
, прямо пропорционально заряду на обкладках конденсатора:  .
.
ЭДС самоиндукции можно представить как вторую производную от заряда по времени:  .
.
Подставляя в закон Кирхгофа, получим:
 (27)
(27)
Разделив обе части этого выражения на  и распределив слагаемые по степени убывания порядка производной, получим дифференциальное уравнение:
и распределив слагаемые по степени убывания порядка производной, получим дифференциальное уравнение: 
Введем стандартные обозначения:  ,
,  .
.
 – собственная частота свободных колебаний в контуре без потерь
– собственная частота свободных колебаний в контуре без потерь  ,
,  – коэффициент затухания в контуре
– коэффициент затухания в контуре 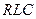 .
.
Уравнение примет стандартный вид:
 (28)
(28)
Это уравнение называется дифференциальным уравнением вынужденных колебаний.
Уравнение (28) является неоднородным линейным дифференциальным уравнением второго порядка. Такого типа уравнения описывают поведение широкого класса колебательных систем (электрических, механических) под влиянием внешнего периодического воздействия (внешней ЭДС или внешней силы). Общее решение уравнения (28) складывается из общего решения соответствующего однородного уравнения
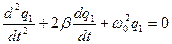 (29)
(29)
и любого частного решения  неоднородного уравнения (28). Характер общего решения однородного уравнения (12) зависит от величины коэффициента затухания
неоднородного уравнения (28). Характер общего решения однородного уравнения (12) зависит от величины коэффициента затухания  . Нас будет интересовать случай слабого затухания:
. Нас будет интересовать случай слабого затухания:  . При этом общее решение уравнения (29) имеет вид (см. затухающие электромагнитные колебания):
. При этом общее решение уравнения (29) имеет вид (см. затухающие электромагнитные колебания):
 (30)
(30)
где  и
и  – постоянные, задаваемые начальными условиями.
– постоянные, задаваемые начальными условиями.
Входящая в (30) величина 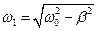 является циклической частотой затухающих колебаний контура:
является циклической частотой затухающих колебаний контура:  определяет амплитуду затухающих колебаний, а
определяет амплитуду затухающих колебаний, а  – их фазу. Решение (30) описывает затухающие колебания в контуре.
– их фазу. Решение (30) описывает затухающие колебания в контуре.
Частное решение уравнения (28) ищем в виде гармонического колебания, происходящего с частотой, равной частоте  внешнего периодического воздействия, и отстающего по фазе на
внешнего периодического воздействия, и отстающего по фазе на  от него.
от него.
 (31)
(31)
где 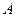 – амплитуда вынужденных колебаний.
– амплитуда вынужденных колебаний.
Подставим (31) в (28), получим тождество  (32)
(32)
Чтобы сравнить фазы колебаний, используем тригонометрические формулы приведения. Тогда (32) перепишется в виде
 (33)
(33)
 Представим складываемые колебания в левой части тождества (33) в виде векторной диаграммы (рис. 6). Если третье слагаемое, соответствующее колебаниям на емкости
Представим складываемые колебания в левой части тождества (33) в виде векторной диаграммы (рис. 6). Если третье слагаемое, соответствующее колебаниям на емкости 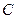 , имеющее фазу
, имеющее фазу  и амплитуду
и амплитуду  , изобразим горизонтальным вектором, направленным вправо. Тогда первое слагаемое левой части, соответствующие колебаниям на индуктивности
, изобразим горизонтальным вектором, направленным вправо. Тогда первое слагаемое левой части, соответствующие колебаниям на индуктивности  , изобразится на векторной диаграмме вектором, направленным горизонтально влево (его амплитуда
, изобразится на векторной диаграмме вектором, направленным горизонтально влево (его амплитуда  ). Второе слагаемое, соответствующие колебаниям на сопротивлении
). Второе слагаемое, соответствующие колебаниям на сопротивлении 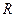 , – вектором, направленным вертикально вверх (его амплитуда
, – вектором, направленным вертикально вверх (его амплитуда  ), т. к. его фаза на
), т. к. его фаза на  отстает от первого слагаемого.
отстает от первого слагаемого.
Так как сумма трех колебаний слева дает гармоническое колебание  , то векторная сумма на диаграмме – (диагональ прямоугольника) изображает колебание с амплитудой
, то векторная сумма на диаграмме – (диагональ прямоугольника) изображает колебание с амплитудой  и фазой
и фазой  , которая на
, которая на  опережает фазу колебаний третьего слагаемого. Из прямоугольного треугольника по теореме Пифагора можно найти амплитуду
опережает фазу колебаний третьего слагаемого. Из прямоугольного треугольника по теореме Пифагора можно найти амплитуду 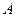 и
и  :
:
 (34)
(34)
 (35)
(35)
следовательно
 (36)
(36)
Общее решение дифференциального уравнения (28) является суммой  и
и  .
.
 (37)
(37)
Формула (37) показывает, что при воздействии на контур периодической ЭДС в нем возникают колебания двух частот: незатухающие колебания с частотой  внешней ЭДС и затухающие колебания с частотой
внешней ЭДС и затухающие колебания с частотой  . Амплитуда затухающих колебаний
. Амплитуда затухающих колебаний  со временем становится пренебрежимо малой, и в контуре остаются только вынужденные колебания, амплитуда которых не зависит от времени. Следовательно, установившиеся вынужденные колебания описываются функцией (31). То есть в контуре возникают вынужденные гармонические колебания, с частотой
со временем становится пренебрежимо малой, и в контуре остаются только вынужденные колебания, амплитуда которых не зависит от времени. Следовательно, установившиеся вынужденные колебания описываются функцией (31). То есть в контуре возникают вынужденные гармонические колебания, с частотой  , равной частоте внешнего воздействия, и амплитудой
, равной частоте внешнего воздействия, и амплитудой  , зависящей от этой частоты по закону (34). При этом по фазе вынужденное колебание отстает на
, зависящей от этой частоты по закону (34). При этом по фазе вынужденное колебание отстает на  от вынуждающего воздействия.
от вынуждающего воздействия.
Продифференцировав выражение (31) по времени, найдем силу тока в контуре
 (38)
(38)
где  – амплитуда тока. Запишем это выражение в виде
– амплитуда тока. Запишем это выражение в виде
 (39)
(39)
где  – сдвиг по фазе между током и внешней ЭДС. В соответствии с (35)
– сдвиг по фазе между током и внешней ЭДС. В соответствии с (35)
 (40)
(40)
Из этой формулы следует, что сдвиг по фазе между током и внешней ЭДС зависит, при постоянном 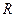 , от соотношения между частотой вынуждающей ЭДС
, от соотношения между частотой вынуждающей ЭДС  и собственной частотой контура
и собственной частотой контура  . Если
. Если  , то сдвиг по фазе между током и внешней ЭДС
, то сдвиг по фазе между током и внешней ЭДС  . Ток в цепи опережает ЭДС на угол
. Ток в цепи опережает ЭДС на угол  . Если
. Если  , тогда
, тогда  . Ток в цепи отстает от ЭДС на угол
. Ток в цепи отстает от ЭДС на угол  . Если
. Если  (резонансная частота), то
(резонансная частота), то  , т. е. ток и ЭДС колеблются в одной фазе.
, т. е. ток и ЭДС колеблются в одной фазе.
Резонанс – это явление резкого возрастания амплитуды при совпадении частоты внешней вынуждающей силы с собственной частотой колебательной системы.
Амплитуду тока можно преобразовать к виду:
 (41)
(41)
 Из этой формулы следует, что амплитуда тока в контуре зависит от частоты внешней ЭДС. График
Из этой формулы следует, что амплитуда тока в контуре зависит от частоты внешней ЭДС. График  представлен на рисунке 3.
представлен на рисунке 3.
С возрастанием  амплитуда тока возрастает, затем достигает максимума, а при дальнейшем увеличении
амплитуда тока возрастает, затем достигает максимума, а при дальнейшем увеличении  асимптотически спадает до нуля. Очевидно, что максимального значения ток достигает при
асимптотически спадает до нуля. Очевидно, что максимального значения ток достигает при  или
или  и равен
и равен  .
.
Напряжение на сопротивлении 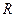 :
:  Разделив выражение на емкость, получим напряжение на конденсаторе
Разделив выражение на емкость, получим напряжение на конденсаторе
 (42)
(42)
Где 
– амплитудное значение напряжения на емкости.
Напряжение на индуктивности  ,
,
 (43)
(43)
где  – амплитудное значение напряжения на дуктивности.
– амплитудное значение напряжения на дуктивности.
Таким образом напряжения на индуктивности и на конденсаторе зависят от частоты внешней ЭДС.
Из (38), (42) и (43) видно, что сдвиг фаз между током и внешней ЭДС при резонансе:
· на активном сопротивлении равен нулю;
· на индуктивности ток  отстает от напряжения
отстает от напряжения  на
на  ;
;
· на емкости ток  опережает
опережает  на
на  .
.
При  возникает резонанс тока. При этом
возникает резонанс тока. При этом  , то есть напряжение на емкости и индуктивности равны по величине и противоположны по фазе. Напряжение на реактивных сопротивлениях точно компенсируют друг друга и, следовательно, ЭДС равна напряжению на активном сопротивлении.
, то есть напряжение на емкости и индуктивности равны по величине и противоположны по фазе. Напряжение на реактивных сопротивлениях точно компенсируют друг друга и, следовательно, ЭДС равна напряжению на активном сопротивлении.
При резонансе  ,
,  . Учитывая, что
. Учитывая, что  , и (20), получим выражения для добротности контура
, и (20), получим выражения для добротности контура
 (44)
(44)
Тогда амплитуды напряжений на индуктивности и емкости можно выразить через собственную добротность:
 (45)
(45)
 (46)
(46)
Из (45), (46) видно, что при  , амплитуда на конденсаторе и индуктивности в
, амплитуда на конденсаторе и индуктивности в  раз больше амплитуды вынуждающей ЭДС. Это свойство последовательного
раз больше амплитуды вынуждающей ЭДС. Это свойство последовательного  контура используется для выделения радиосигнала определенной частоты
контура используется для выделения радиосигнала определенной частоты  из спектра радиочастот при перестройке радиоприемника.
из спектра радиочастот при перестройке радиоприемника.
Реальные  контура связаны с другими контурами, измерительными приборами или усилительными устройствами, вносящими дополнительное затухание в
контура связаны с другими контурами, измерительными приборами или усилительными устройствами, вносящими дополнительное затухание в  контуре. Поэтому реальная величина добротности нагруженного
контуре. Поэтому реальная величина добротности нагруженного  контура оказывается ниже величины добротности, оцениваемой
контура оказывается ниже величины добротности, оцениваемой  . Реальная величина добротности может быть оценена как
. Реальная величина добротности может быть оценена как
 (47)
(47)
где  – ширина полосы частот, в которых амплитуда тока составляет 0,7 от максимального значения.
– ширина полосы частот, в которых амплитуда тока составляет 0,7 от максимального значения.
Приложение 4
ВОЛНЫ
Механические волны
Упругой средой называется среда, частицы которой связаны между собой упругими силами. Например, газу присуща объемная упругость, то есть способность сопротивляться изменению его объема. Это свойство газа обусловлено тепловым движением молекул газа и проявляется в изменении давления газа р при изменении его объема V. Если какая-либо точка упругой среды начинает совершать механические колебания, то энергия колебания этой точки будет передаваться окружающим точкам, вызывая их колебания.
Механические колебания, распространяющиеся в упругой среде, называются упругими или механическими волнами.
Геометрическое место точек, до которых к данному моменту времени дошли колебания, называется фронтом волны. Геометрическое место точек, в которых фаза колебаний имеет одно и то же значение, называется волновой поверхностью. Очевидно, что фронт волны является одной из волновых поверхностей.
Среда называется изотропной, если её свойства одинаковы во всех направлениях. В такой среде колебания распространяются по всем направлениям с одной и той же скоростью. Волновые поверхности в случае точечного источника колебаний являются сферами с центром в источнике колебаний. Волна называется плоской, если ее волновые поверхности представляют совокупность плоскостей, параллельных друг другу.
Упругая волна называется продольной, если точки среды колеблются в направлении распространения волны. Продольные волны обусловлены объемной упругостью среды и могут распространяться в любой среде – твердой, жидкой, газообразной. Примером таких волн являются звуковые волны в воздухе. Волна, колебания в которой совершаются в направлении, перпендикулярном направлению распространения волны, называется поперечной волной. Примером поперечных волн могут служить волны, распространяющиеся вдоль струн музыкальных инструментов.
Звуком, звуковыми или акустическими волнами называются упругие волны малой интенсивности, распространяющиеся в упругой среде. Звуковые волны частотой от 16 Гц до 20 кГц – слышимые звуки, менее 16 Гц – инфразвук, более 20 кГц – ультразвук. Воспринимаемые звуки люди различают по громкости, высоте и тембру. Громкость определяется интенсивностью звуковой волны, пропорциональной ее амплитуде. Любой реальный звук является наложением колебаний с определенным набором частот, называемым акустическим спектром. Сплошным спектром обладают шумы. Звук с линейчатым спектром слышится как звук с определенной частотой. Высота определяется основной или наименьшей частотой. Относительная интенсивность волн с другими частотами определяет тембр звука.
Получим уравнение бегущей волны. Пусть волна распространяется вдоль оси OX от источника колебаний, находящегося в начале координат – точке О. Все точки на оси OX будут повторять колебания точки О с некоторым запозданием во времени. Но закон движения для них будет одинаков, то есть они будут в отсутствии потерь энергии колебаться с одной и той же частотой и одинаковой амплитудой. Точка О совершает гармоническое колебание, смещение точки О описывается законом:
 (1)
(1)
Здесь обозначено: 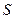 – смещение точки О,
– смещение точки О, 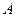 – амплитуда,
– амплитуда,  – циклическая частота колебаний,
– циклическая частота колебаний,  – время, отсчитанное от вступления точки О в колебание.
– время, отсчитанное от вступления точки О в колебание.
В упругой волне все точки среды, расположенные вдоль оси OX, не перемещаются, а совершают колебания с циклической частотой  вокруг собственных положений равновесия.
вокруг собственных положений равновесия.  – это смещение точки с координатой
– это смещение точки с координатой  в момент времени
в момент времени  от своего собственного положения равновесия. В монохроматической волне амплитуды и частоты колебаний всех точек одинаковы, а фазы разные. Для произвольной точки
от своего собственного положения равновесия. В монохроматической волне амплитуды и частоты колебаний всех точек одинаковы, а фазы разные. Для произвольной точки  на оси OX уравнение колебаний имеет вид:
на оси OX уравнение колебаний имеет вид:

где  – время, отсчитанное от начала вступления точки
– время, отсчитанное от начала вступления точки  в колебательный процесс. Эта точка начала колебаться позднее, чем точка О на время τ, поэтому
в колебательный процесс. Эта точка начала колебаться позднее, чем точка О на время τ, поэтому  . Если скорость распространения волны
. Если скорость распространения волны  , тогда
, тогда  , где
, где  – координата рассматриваемой точки. Тогда уравнение можно переписать в виде:
– координата рассматриваемой точки. Тогда уравнение можно переписать в виде:
 (2)
(2)
Фаза волны 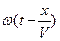 зависит от времени и координаты. Смещение
зависит от времени и координаты. Смещение 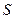 является периодической функцией двух переменных: времени
является периодической функцией двух переменных: времени  и координаты
и координаты  . Значит, волновой процесс – это периодический процесс, повторяющийся во времени и пространстве.
. Значит, волновой процесс – это периодический процесс, повторяющийся во времени и пространстве.
Длиной волны называется расстояние, на которое волна распространяется за период:

Если ввести понятие волнового числа 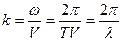 , то уравнение бегущее вдоль оси ОХ волны примет вид:
, то уравнение бегущее вдоль оси ОХ волны примет вид:
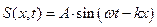 (3)
(3)
 Стоячей волной называется волна, образующаяся в результате наложения двух волн, которые распространяются навстречу друг другу и имеют одинаковые частоты и амплитуды, а в случае поперечной волны еще и одинаковую поляризацию. Стоячую звуковую волну можно получить следующим образом. Возьмем стеклянную трубу длиной
Стоячей волной называется волна, образующаяся в результате наложения двух волн, которые распространяются навстречу друг другу и имеют одинаковые частоты и амплитуды, а в случае поперечной волны еще и одинаковую поляризацию. Стоячую звуковую волну можно получить следующим образом. Возьмем стеклянную трубу длиной  (рис. 1), закрытую с одной стороны. У открытого конца трубы будем возбуждать гармоническое колебание воздуха (включим звуковой генератор).
(рис. 1), закрытую с одной стороны. У открытого конца трубы будем возбуждать гармоническое колебание воздуха (включим звуковой генератор).
Вдоль трубы будут распространяться звуковые волны; дойдя до закрытого конца, волны отразятся и будут распространяться в сторону открытого конца. Падающие и отраженные волны накладываются, интерферируют, и в трубе образуются стоячие волны.
Выведем уравнение стоячей волны. Уравнение падающей волны  для точки М имеет вид (2). Уравнение отраженной волны для той же точки:
для точки М имеет вид (2). Уравнение отраженной волны для той же точки:

Знак «минус» учитывает перемену фазы на противоположную при отражении звуковой волны от более плотной среды (воздух-стекло). Результирующее смещение для точки  будет равно:
будет равно:

Используя формулу разности синусов:
 ,
,
получим уравнение стоячей волны:
 (4)
(4)
Абсолютное значение множителя  , не зависящего от времени, является амплитудой стоячей волны.
, не зависящего от времени, является амплитудой стоячей волны.
Точки, смещение которых все время равно нулю называются узлами стоячей волны. Найдем координаты узлов. Для этого запишем уравнение:



где  ; учитывая, что,
; учитывая, что,  запишем:
запишем:
 ,
,
Координаты нулевого, первого, второго, n-го узлов:
 ,
,  ,
,  ,
, 
У закрытого конца трубы образуется узел и все узлы расположены на расстоянии полуволны друг от друга.
Точки, для которых  имеют максимальную амплитуду, равную 2А. Эти точки называются пучностями стоячей волны. Найдем их координаты. Для этого положим:
имеют максимальную амплитуду, равную 2А. Эти точки называются пучностями стоячей волны. Найдем их координаты. Для этого положим:



Учитывая, что  , запишем:
, запишем: 
Координаты узлов смещения:


 .
.
Пучности расположены на расстоянии полуволны друг от друга. Множитель  показывает, что все точки в стоячей волне совершают гармонические колебания с периодом Т.
показывает, что все точки в стоячей волне совершают гармонические колебания с периодом Т.
Условия отражения от границы раздела сред: если среда, от которой происходит отражение, более плотная, чем среда в которой волна распространяется, то на границе получается узел смещения. Это объясняется тем, что волна, отражаясь от более плотной среды, в месте отражения меняет свою фазу на противоположную. Это явление называется отражением с «потерей полуволны». Отражаясь от менее плотной среды, волна не меняет фазы в месте отражения, потери полуволны не происходит. Фазы падающей и отраженной волн у границы одинаковы и в этом месте получается пучность смещения в результате сложения колебаний одинаковых фаз.
Не нашли, что искали? Воспользуйтесь поиском: