Затухающие механические колебания

Свободные колебания реальных механических систем всегда затухают. Затухание возникает в основном из-за трения, сопротивления окружающей среды и возбуждения в ней упругих волн.

Рассмотрим систему, совершающую крутильные затухающие колебания. Она представляет из себя брусок, подвешенный на струне, концы которой закреплены. На брусок для увеличения момента инерции может быть положен брусок. После отклонения бруска на небольшой угол от положения равновесия система будет совершать свободные крутильные колебания.

Получим дифференциальное уравнение затухающих крутильных колебаний. Чтобы выяснить, как изменяется со временем 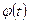используем основной закон динамики вращательного движения:

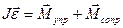(1)

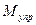Где – момент инерции бруска, – угловое ускорение, – момент сил упругости, – момент сил сопротивления.

, – коэффициент упругости. Для малых скоростей вращения , – коэффициент сопротивления, – угловая скорость. Уравнение (1) в скалярной форме примет вид:

Обозначив ( – коэффициент затухания) и ( – циклическая частота свободных незатухающих колебаний), получим

(2)

Решением этого уравнения при малом затухании является функции:

(3)

Здесь – амплитуда в начальный момент времени, – амплитуда затухающих колебаний.

Циклическая частота затухающих колебаний:

(4)

Быстроту затухания колебаний принято характеризировать логарифмическим декрементом затухания:

(5)

Где и – амплитуды двух соседних колебаний. Или для колебаний:

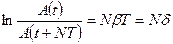(6)

Выясним физический смысл коэффициента затухания. Обозначим через 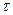время, в течении которого амплитуда колебаний уменьшается в раз.

Тогда ,

а следовательно, и

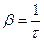(7)

Отсюда ясен физический смысл коэффициента затухания: коэффициент затухания есть величина, обратная времени, за которое амплитуда колебаний уменьшается в e раз.

Физический смысл логарифмического декремента затухания:

(8)

Где – число колебаний, происходящих за время 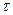. Таким образом, логарифмический декремент есть величина, обратная числу колебаний, по завершению которых амплитуда уменьшается в раз .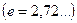

Определим период затухающих колебаний. Выразим циклическую частоту затухающих колебаний и циклическую частоту собственных колебаний через соответствующие периоды 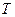и : 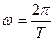, . Учитывая, что коэффициент затухания связан с логарифмическим декрементом затухания отношением: из формулы (4) следует: , отсюда .

Из выражения для собственной частоты крутильных колебаний можно выразить период собственных крутильных колебаний: , тогда период затухающих колебаний бруска:

(9)

Если на брусок положить кольцо, момент инерции, то добавится момент инерции, создаваемый кольцом , где – масса кольца, – его радиус.

Для периода крутильных колебаний системы с кольцом:

(10)

Возьмем отношение и получим из нее расчетную формулу для момента инерции бруска:

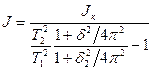(11)

Если и то можно записать приближенную формулу:

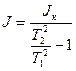(12)

Определив периоды колебаний и , момент инерции кольца , можно определить момент инерции бруска .

Не нашли, что искали? Воспользуйтесь поиском: