Е уравнение Максвелла

Является обобщением закона электромагнитной индукции Фарадея. Всякое изменяющееся во времени магнитное поле создает в пространстве вихревое электрическое поле , циркуляция которого по произвольному контуру определяет электродвижущую силу в этом контуре. Для электростатического (потенциального) электрического поля такая циркуляция равна нулю.

Интегральная форма уравнения:

.

Циркуляция вектора напряженности электрического поля по любому контуру равна со знаком минус производной по времени от потока индукции магнитного поля через любую поверхность 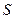, опирающуюся на контур . При этом под вектором понимается не только вихревое, но и электростатическое поле .

Дифференциальная форма уравнения:

.

Ротор вектора напряженности электрического поля в любой точке поля равен скорости уменьшения во времени вектора в этой точке

2-е уравнение Максвелла.

Является обобщением закона полного тока (теоремы о циркуляции вектора напряженности магнитного поля). Всякое изменяющиеся во времени электрическое поле наряду с током проводимости создает в пространстве вихревое магнитное поле.

Интегральная форма уравнения:

.

Циркуляция вектора напряженности магнитного поля по любому контуру равна сумме потока вектора плотности тока проводимости и потока вектора плотности тока смещения через произвольную поверхность 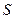, опирающуюся на контур . Напомним, что поток вектора плотности тока есть ток, так что справа стоит сумма токов проводимости и смещения, охватываемых контуром : – ток проводимости.

Дифференциальная форма уравнения:

.

Ротор вектора напряженности магнитного поля в любой точке пространства равен сумме векторов плотности тока проводимости и плотности тока смещения .

3-е уравнение Максвелла.

Является формулировкой теоремы Гаусса для вектора индукции электрического поля 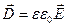. Векторные линии индукции начинаются и заканчиваются только на свободных (сторонних) зарядах. В то время как источником электрического поля являются свободные и связанные заряды.

Интегральная форма уравнения:

.

Поток вектора индукции электрического поля через произвольную замкнутую поверхность 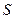равен суммарному свободному электрическому заряду, расположенному внутри этой замкнутой поверхности 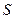(ограничивающей объем ). Справа – объемный интеграл от объемной плотности свободного электрического заряда.

Дифференциальная форма уравнения:

.

Дивергенция вектора индукции электрического поля в любой точке равна объемной плотности свободного электрического заряда в этой точке.

Не нашли, что искали? Воспользуйтесь поиском: